Salut,
b) Ça serait pas bète de noter différement des fonctions... différentes... donc on va dire que la fonction de densité de X on la note f et celle de Y, on la note g.
a) Il manque cruellement une information concernant l'indépendance entre les v.a.r. X et Y donc... je suppose qu'elles sont indépendantes, sinon on ne peut rien savoir sur la loi de X/Y.
Dans ce cas (indépendance), la fonction de densité du couple
)
, c'est simplement
g(y))
, c'est à dire que la proba que le couple
)
soit dans une partie A donnée de R² est
\in A\big)=\int\int_A f(x)g(y)\, dxdy)
.
En pour
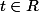
fixé
=p\big(\frac{X}{Y}\leq t\big)=\int\int_{A_t} f(x)g(y)\, dxdy\)
où
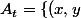\in{\mathbb R}^2\text{ t.q. }\frac{x}{y}\leq t\})
Vu les fonctions

et

il suffit de calculer l'intégrale sur

.
Si
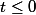
alors
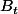
est vide donc
=0)
(ce qui était évident dés le départ)
Si

alors
\in B_t\ \Leftrightarrow\ 0\frac{x}{t}\)
donc (Fubini) :
=\int_0^1f(x)\Big(\int_{\frac{x}{t}}^\infty g(y)\,dy\Big)dx)
que tu peut soit calculer bètement puis dériver pour avoir la densité, soit dériver directement (dérivation sous le signe somme)...