J'ai cet énoncé de variables aléatoires :
Trois urnes contient chacune n boules numérotées de 1 à n, on tire une boule de chaque urne et on note trois variables aléatoires :
Et on veut calculer la loi du triplet
Merci
GaBuZoMeu a écrit:Bonjour,
Combien y a-t-il de tirages en tout ?
Ensuite, fixe trois entierstels que
. Combien y a-t-il de tirages tels que
? Bien sûr, il faut discuter selon que les
dont distincts, ou s'il y en a deux d'égaux, ou s'il sont tous les trois égaux.
tournesol a écrit:Bonjour
Quelle est la définition du milieu pour (5;5;6) ?
En principe le max et sans ambiguité, le min non plus , donc le milieu est l'autre composante du triplet donc 5 ???
matheuxendetresse a écrit:GaBuZoMeu a écrit:Bonjour,
Combien y a-t-il de tirages en tout ?
Ensuite, fixe trois entierstels que
. Combien y a-t-il de tirages tels que
? Bien sûr, il faut discuter selon que les
dont distincts, ou s'il y en a deux d'égaux, ou s'il sont tous les trois égaux.
Merci,
(On fait le tirage des boules des trois urnes une seule fois)
J'ai essayé de le définir comme une suite, et j'ai trouver que siest le nombres des boules dans chacune des urnes, alors la suite
est le nombre des états possibles (qui doivent être équiprobables) : et je l'ai conjecturée ainsi:
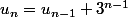
Dont on peut trouver la formule explicite facilement (or est-ce c'est correcte?)
Ben314 a écrit:Salut,
Je comprend pas ce que tu bricole.
Si on noteles variables aléatoire correspondant aux numéros tirés dans les urne 1,2,3, alors il me semble clair que le triplet
prend ses valeurs dans l'ensemble
(et que tout les cas sont équiprobable) ce qui fait évidement
cas possible.
Ensuite, ce qu'il faut que tu cherche, c'est, pourdonnés tels que
, combien il y a de triplets
tel que le min des 3 soit
, le milieu
et le max
.
Combien y-a-t'il de triplettel que le min soit 3, le milieu 3 et le max 5 ?
Ben314 a écrit:Pourquoi "fois 2" ?
Ben314 a écrit:Oui, c'est ça.
Et si ça t'amuse (et/ou que tu veut t’entraîner à ce type de calculs), tu peut vérifier que la somme des probas fait 1 en dénombrant le nombre de cas qu'il y a dans chacune de tes 4 catégories.
Ben314 a écrit:Je ne sais pas comment tu as fait ton calcul, mais ça se simplifie bien plus que ça normalement vu que c'est du simple dénombrement immédiat avec les coefficients binomiaux.
Mais ton truc est sans doute bon, modulo de calculer explicitement la valeur de ta somme (ce qui est très facile vu la somme)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :