Antho07 : merci pour l'exo 5, mais en fait quand je veux le faire pour u1 à u4, ben j'obtiens toujours une famille libre :s
Je crois qu'il faut poser
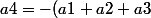)
mais je ne comprends pas pourquoi. Est ce que c'est juste une conséquence du système ? Et dans ce cas pourquoi n'est ce pas la même chose pour le cas précédent (celui que tu as détaillé).
Ptiboudelard : la base canonique pour la question 1 ça serait u = (1, 0) v = ( 0, 1) alors ? Mais la dimension étant 4 d'après la formule, mes vecteurs ne devraient pas être de la forme vecteur (a, b, c, d) avec a, b, c, d rééls ? Je dis surement une énormité, mais c'est flou pour moi.
Pour la question 2, je ne vois pas comment cela sert à démontrer que M est un sev : dans mon cours un sev doit justifier deux propriétés : pour x et y 2 vecteurs de mon sev, x = y doit appartenir à ce sev et le résultat de la multiplication d'un réel par un vecteur de ce sev doit appartenir à ce sev. La deuxième propriété est justifiée car la matrice libre appartient à M, mais pour la première ?
Pour la troisième question : mettre des vecteurs en facteurs... euh...oui mais comment ? Genre j'ai deus vecteur (a, b) et (c, a) ? Mais je sais pas quoi en faire ensuite :/
