Groupes anneaux corps
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Impiger
- Membre Naturel
- Messages: 77
- Enregistré le: 25 Oct 2009, 19:41
-
 par Impiger » 22 Déc 2010, 12:12
par Impiger » 22 Déc 2010, 12:12
Bonjour j'ai un petit exo qur les groupes , qui n'est pas bien compliqué je pense mais je 'en saisis pas tout à fait l'énoncé.
Soit (G , . ) un groupe fini tel que quel que soit x de G, x²=e où e est l'élément neutre de G.
1) Montrer que G est commutatif. Là aucun problème.
2)Soit H un sous-groupe de G et soit a un élément de G n'appartenant pas à H.
Montrer que H inter aH = O (ensemble vide)
que H U aH est un sous-groupe de GC'est là mon problème car je ne comprends pas ce que "signifie" ou représente aH car a est un élément et H un ensemble.
3) En déduire que card G est une puissance de 2; eT alors là , je ne vois pas le rapport et donc ne sais absolument pas comment faire!
Merci beaucoup !
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 22 Déc 2010, 12:13
par arnaud32 » 22 Déc 2010, 12:13
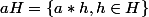
si
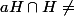
soit
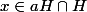
donc
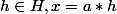
et tu as
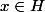
comme H est un sous groupe
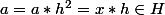
ce qui est absurde
on a
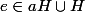
et
soit x et y
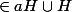
tu as x=b*h et y=b'*h' avec
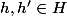
et
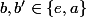
*(h*h'))
par commutativite
de plus
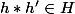
et
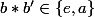
de plus
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 22 Déc 2010, 15:52
par arnaud32 » 22 Déc 2010, 15:52
pour le dernier
si G={e}

sinon tu notes
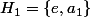
qui est un sous groupe de G
si
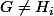
tu sais que
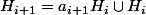
est un sous groupe de G pour
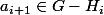
tu as en outre
+#(H_i)=2#(H_i))
car
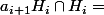
tu en deduis que

et comme g est fini, il y a un rang ou
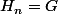
-
nix386
- Membre Naturel
- Messages: 69
- Enregistré le: 11 Déc 2010, 12:39
-
 par nix386 » 22 Déc 2010, 17:22
par nix386 » 22 Déc 2010, 17:22
elle est ou l absurdité ici ?

-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 22 Déc 2010, 17:26
par arnaud32 » 22 Déc 2010, 17:26
a est un element de G qui n'apartient pas à H ... par hypothese
-
Impiger
- Membre Naturel
- Messages: 77
- Enregistré le: 25 Oct 2009, 19:41
-
 par Impiger » 22 Déc 2010, 18:05
par Impiger » 22 Déc 2010, 18:05
d'accord merci, j'ai bien compris le début, mais je ne saisis pas ce que représente ton dièse # est-ce que c'est la notation du cardinal. Dans ce cas j'ai tout compris : merci beaucoup !
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 23 Déc 2010, 09:19
par arnaud32 » 23 Déc 2010, 09:19
oui c'est exactement ca
-
Impiger
- Membre Naturel
- Messages: 77
- Enregistré le: 25 Oct 2009, 19:41
-
 par Impiger » 26 Déc 2010, 13:37
par Impiger » 26 Déc 2010, 13:37
Alors merci vraiment infiniment !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités

