Fonction de complexes

[aurelie1584]

Bonjour

voici une question d'un exercice sur les complexes qui me pose des problemes, merci de m'aider:

On note f l'application de dans lui me^me définie par
et F l'application de P\{0} (un plan) dans lui même qui, à un point M d'affixe Z, associe le point d'affixe f(z)

résoudre dans C* les équations f(z)=z et f(f(z))=z
determiner les point P\{0} invariants par F

[Ericovitchi]

écris tout simplement les équations. Qu'est-ce qui te bloque ?
f(z)=z --> 1/z²=z les 3 racines cubique de l'unité !
f(f(z))=z --> z4=z

[Nightmare]

Salut,

tu n'arrives pas à résoudre les équations?

Il s'agit de résoudre 1/z²=z et 1/z^4 = z, rien de bien compliqué à priori, ce sont des racines de l'unité !

[Ericovitchi]

attention f(f(z))=z^4 et pas 1/z^4

[Nightmare]

attention f(f(z))=z^4 et pas 1/z^4

Merci pour la coquille.

[aurelie1584]

oui je dois paniquer devant les notation je vais regarder ca tranquillement
merci

[aurelie1584]

Oui en fait c'était vraiment simple. par contre si quelqu'un est inspiré par cel ce serait vraiment cool :

On note la droite d'équation
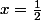
Si M un point du plan , on note M' son projeté orthogonal sur
On note alors P l'ensemble de spoints M du plan pour lesquels OM=MM' (ce n'est pas le même p)

a) montrer qu'un point M du plan de coordonnées (x,y) appartient à P ssi

b) on considere M un point de P on note Z son affixe , le module de Z et un argument
Montrer que , puis que

[Nightmare]

Il te suffit de traduire l'égalité OM=MM' avec les affixes de O, M et M'.

OM=|z| et MM'=|z'-z| où z et z' sont respectivement les affixes de M et M'. Mais comme M' est le projeté orthogonal de M sur la droite d'équation x=1/2 il est clair (schéma si nécessaire) que z'=1/2+ iy avec z=x+iy donc MM'=|1/2 - x|

je te laisse conclure.

[aurelie1584]

Il te suffit de traduire l'égalité OM=MM' avec les affixes de O, M et M'.

OM=|z| et MM'=|z'-z| où z et z' sont respectivement les affixes de M et M'. Mais comme M' est le projeté orthogonal de M sur la droite d'équation x=1/2 il est clair (schéma si nécessaire) que z'=1/2+ iy avec z=x+iy donc MM'=|1/2 - x|

je te laisse conclure.

merci beaucoup !! vous auriez une idée pour l'autre question ?? je vois ce qu'il fauut trouver. je pense qu'il faudra utiliser a un moment l'expression
mais je n'arrive pas a démarrer mon calcul.
Encore merci

[Ben314]

Salut,
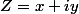
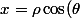Dire que est le module de Z et que est un argument de Z signifie que , c'est à dire que où et .
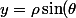De plus, tu as montré au a) que M est dans P ssi ce qui, exprimé en terme de et signifie que... (qui est une équation du second degrés en que l'on résoud... comme une équation du second degrés...)