Polynome et complexes

par **wserdx** » 23 Oct 2012, 21:59

Bon, on va faire simple.
Il s'agit d'une somme de monômes en une même indéterminée, ici X.
Chaque monôme est une expression formelle, qui peut s'évaluer quand on remplace l'indéterminée par une autre expression formelle ou numérique.
Exemple
Si

alors

.
Mais aussi par exemple

Ou aussi

Tu vois mieux où je veux en venir ?

par **Rockleader** » 23 Oct 2012, 22:06

wserdx a écrit:Bon, on va faire simple.
Il s'agit d'une somme de monômes en une même indéterminée, ici X.
Chaque monôme est une expression formelle, qui peut s'évaluer quand on remplace l'indéterminée par une autre expression formelle ou numérique.
Exemple
Si
alors.
Mais aussi par exemple
Ou aussi
Tu vois mieux où je veux en venir ?

Le module de j vaut 1 ? Ce qui expliquerait que j^4 = j dans ton équation ?

Mais je vois pas vraiment à quoi ça nous amène...

par **wserdx** » 23 Oct 2012, 22:14

était celui défini dans ton exercice, soit

ça nous amène à te demander : comment évalues-tu

et

à partir de l'expression fournie dans ton exercice ?

par **Rockleader** » 23 Oct 2012, 22:22

wserdx a écrit: était celui défini dans ton exercice, soit
ça nous amène à te demander : comment évalues-tu et à partir de l'expression fournie dans ton exercice ?

Pour moi : j = e^2ipi/3 et j²= e^4ipi/3

P(X) = ao + a1X + ... + akX^k
P(jX) aoj + a1jX + ... + akjX^K
P(j²X)= aoj² + a1j²X + ... + akj²X^k

On aurait donc P(j²X) = 2 P(jX) ???

Si on considère que j=1 (ce que j'ai cru comprendre avec ton exemple)

Alors P(j²X) = P(jX)

par **wserdx** » 23 Oct 2012, 22:28

Visiblement, tu ne sais pas évaluer un polynôme. Je vais avoir du mal à t'aider.
Si

, où

est une constante et

un entier, que vaut

?

par **Rockleader** » 23 Oct 2012, 22:34

wserdx a écrit:Visiblement, tu ne sais pas évaluer un polynôme. Je vais avoir du mal à t'aider.
Si , où est une constante et un entier, que vaut ?

Pour commencer qu'est ce que tu entend exactement par évaluer un polynome ? Parce que pour savoir comment faire il faudrait déjà que je sache ce que ça veut dire...

Je ne saurais pas te dire ce que vaut Q(jX) puisque apparemment toutes mes tentatives précédentes était fausse...je ne vais pas continuer à faire des proposition hasardeuses sans avoir une vrai définition..

par **Rockleader** » 23 Oct 2012, 22:42

J'ai trouvé dans mon cours que

si P(X) = a0 +...+ anXn

Alors (bP)(X) = (ba0) + (ba1)X +...+ (ban)Xn

Donc je comprends pourquoi j'ai faux bP(X) n'est pas égal à P(bX)

Mais dans ce cas là je ne sais pas comment faire...

par **wserdx** » 23 Oct 2012, 22:50

Évaluer un polynôme c'est donner la valeur de l'expression du polynôme pour un argument donné.
Par exemple évaluer

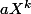
en

, c'est donc simplement

Dans ton exercice si

alors

Je te laisse faire pour

....

par **wserdx** » 23 Oct 2012, 22:52

Rockleader a écrit:J'ai trouvé dans mon cours que

si P(X) = a0 +...+ anXn

Alors (bP)(X) = (ba0) + (ba1)X +...+ (ban)Xn

Donc je comprends pourquoi j'ai faux bP(X) n'est pas égal à P(bX)

Mais dans ce cas là je ne sais pas comment faire...

Je comprends ta méprise.

par **Rockleader** » 23 Oct 2012, 22:58

wserdx a écrit:Évaluer un polynôme c'est donner la valeur de l'expression du polynôme pour un argument donné.
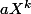
Par exemple évaluer en , c'est donc simplement
Dans ton exercice si
alors

Je te laisse faire pour ....

Daccord, on se comprends déjà mieux.

Par contre, on s'arrête à k=n donc pas besoin de mettre anj^nX^n non ?

Donc P(j²X)= ao + a1j²X + a2j^3X² + ... + akj^(k+1)X^k ?

Bon j'arrête pour ce soir, je dois etre en cours pour 7h45, je vais avoir la tete comme une pastèque si je continue.

Merci pour ton aide préscieuse !

par **wserdx** » 23 Oct 2012, 23:06

Pour l'indice k, il est "formel", comme n, d'ailleurs. C'est à dire que n représente n'importe quel nombre. k représente n'importe quel nombre compris entre 0 et n. (que d'abstraction ! :lol3: )
Bon, pour

, ce n'est pas encore ça :triste: . La nuit porte conseil !

par **Rockleader** » 24 Oct 2012, 06:14

ao + a1X + a2j²X²+...+akj^kX^k ? Mais je crois pas que ce soit ça non plus..j'ai pas compris ce qui n'allait pas dans ma dernière proposition...

par **wserdx** » 24 Oct 2012, 06:27

Faut procéder par étapes.
Évalue

en

c'est à dire remplace

par

dans

par **Rockleader** » 24 Oct 2012, 10:12

wserdx a écrit:Faut procéder par étapes.
Évalue en c'est à dire remplace par dans

J'ai eu un éclair de génie pendant mon cours d'info (oui je travaillais encore mon dm de math pendant mon cours d'info :hum: )

Enfin bref, je sais pas si c'est bon ou pas, mais ça e semble plus correct

P(j²(X) = ao + a1j²X + a2j^4X² + .. + ak j^(2k) X^k

Car c'est (j²X) qui est élevé à la puissance et pas seulement X

Etait ce bien un éclair de génie ? Ou bien était ce de la folie ? =)

(l'un pouvant aller avec l'autre^^)

par **wserdx** » 24 Oct 2012, 10:22

Bon, on y est presque! Continue. Somme

.
Utilise également une variable pour le degré du polynôme (n,m ce que tu veux...) et une autre (k ou autre) pour l'indice variable variant de 0 jusqu'au degré, ça clarifie la compréhension.

par **Rockleader** » 24 Oct 2012, 11:06

wserdx a écrit:Bon, on y est presque! Continue. Somme .
Utilise également une variable pour le degré du polynôme (n,m ce que tu veux...) et une autre (k ou autre) pour l'indice variable variant de 0 jusqu'au degré, ça clarifie la compréhension.

Quand tu dis que j'y suis presque, j'ai trouvé la bonne expression de P(j²X) ?

En fait tu voudrais que je termine le polynome par akj^2kX^k + ... + anj^2nX^n ?

Mais ici on a n=k alors, c'est pas très utile nan ?

par **wserdx** » 24 Oct 2012, 11:20

Rockleader a écrit:Quand tu dis que j'y suis presque, j'ai trouvé la bonne expression de P(j²X) ?

En fait tu voudrais que je termine le polynome par akj^2kX^k + ... + anj^2nX^n ?

Mais ici on a n=k alors, c'est pas très utile nan ?

Oui, c'est ça pour P(j^2X).
Pour k, je ne vois pas très bien ce que tu veux dire par k=n. k prend toutes les valeurs de 0 à n.
Dans cette écriture

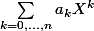
k et n sont deux variables de signification différentes. Mais c'est un point de détail, tu y réfléchiras plus tard...

par **Rockleader** » 24 Oct 2012, 11:29

wserdx a écrit:Oui, c'est ça pour P(j^2X).
Pour k, je ne vois pas très bien ce que tu veux dire par k=n. k prend toutes les valeurs de 0 à n.
Dans cette écriture

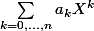
k et n sont deux variables de signification différentes. Mais c'est un point de détail, tu y réfléchiras plus tard...

Ah oui bien sur, j'ai lu trop vite la première fois...k=n ce serait seulement la dernière valeur de k...l vaut 0 au départ.

Donc maintenant, il me faut faire la somme des expressions que j'ai enfin trouvé. Mais je ne vois pas bien comment ça va se passer...ou plutot qu'est ce que l'on cherche à déterminer en faisant la somme.

Il faudrait que je tente de factoriser le tout par X^k de manière à trouver ck, mais je vois pas très bien ce que ça peut donner

par **Rockleader** » 24 Oct 2012, 15:09

Bon, alors j'y ai réfléchi pendant mes 2h de math et je pense avoir trouver un début de solution

D'après les expressions que j'ai donné précédemment des Polynomes

On aurait

EN sommant et divisant par 3 à gauche j'obtiens

ao +a1X ( 1 + j +j²) + a2X²(1+j²+j^4) + ... + anX^n ( 1 + j^n + j^2n)

Or on a trouvé en 1 que si n multiplique de 3, 1+j^n+j^2n vaut 3, sinon vaut 0

ao + 3a1X + ... + 3anX^n (n étant supposé multiple de 3 dans l'énoncé)

Ck = 3 an

Voilà, je ne sais pas si c'est la bonne réponse mais je trouve ça plutot logique.

Je bloque toujours sur la suite.

par **wserdx** » 24 Oct 2012, 16:51

A mon avis tu t'emmêles toujours les pinceaux avec n=k (blocage cérébral?).
Fixe par exemple

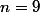
et calcule

.

Polynome et complexes

Qui est en ligne