Nombres complexes - structures algébriques - Algèbre linéair
60 messages
- Page 2 sur 3 - 1, 2, 3
Si la somme n'est pas directe, la décomposition x = f + g n'est pas unique et donc l'image s(x) = f - g ne l'est pas non plus. Du coup, s n'est pas bien définie.
C'est la même chose avec les projections. La projection sur F parallèlement à G est définie par:
p(x) = f
Si la somme n'est pas directe, la projection est mal définie.
On dit que F et G sont en somme directe si l'intersection de F et G ne contient que 0. On peut d'ailleurs remarquer qu'elle contient forcément 0 car F et G sont des espaces vectoriels.
Cette condition est par ailleurs équivalente à la condition suivante:
Pour tout x dans E, il existe un unique f dans F et un unique g dans G tel que x = f + g.
Pour montrer ce truc là, ce n'est pas bien compliqué.
Supposons que la première condition soit vraie.
On suppose que x s'écrit de deux manières différentes: x = f_1 + g_1 = f_2 + g_2
Alors: f_1 - f_2 = g_2 - g_1
Donc f_1 - f_2 appartient à la fois à F et G donc vaut 0. D'où f_1 = f_2.
Et de même, g_1 = g_2.
Supposons que la deuxième condition soit vraie.
On se donne x qui appartient à la fois à F et à G.
Tu sais que x = f + g avec f dans F et g dans G uniques.
Donc x + 0 = f + g.
0 est dans G donc par unicité, g = 0.
Donc: x = f
Mais: 0 + x = f + 0
Le 0 de gauche appartien à F, x appartient à G, f appartient à F et 0 appartient à G.
Par unicité, x = 0.
C'est la même chose avec les projections. La projection sur F parallèlement à G est définie par:
p(x) = f
Si la somme n'est pas directe, la projection est mal définie.
On dit que F et G sont en somme directe si l'intersection de F et G ne contient que 0. On peut d'ailleurs remarquer qu'elle contient forcément 0 car F et G sont des espaces vectoriels.
Cette condition est par ailleurs équivalente à la condition suivante:
Pour tout x dans E, il existe un unique f dans F et un unique g dans G tel que x = f + g.
Pour montrer ce truc là, ce n'est pas bien compliqué.
Supposons que la première condition soit vraie.
On suppose que x s'écrit de deux manières différentes: x = f_1 + g_1 = f_2 + g_2
Alors: f_1 - f_2 = g_2 - g_1
Donc f_1 - f_2 appartient à la fois à F et G donc vaut 0. D'où f_1 = f_2.
Et de même, g_1 = g_2.
Supposons que la deuxième condition soit vraie.
On se donne x qui appartient à la fois à F et à G.
Tu sais que x = f + g avec f dans F et g dans G uniques.
Donc x + 0 = f + g.
0 est dans G donc par unicité, g = 0.
Donc: x = f
Mais: 0 + x = f + 0
Le 0 de gauche appartien à F, x appartient à G, f appartient à F et 0 appartient à G.
Par unicité, x = 0.
egan a écrit:Si la somme n'est pas directe, la décomposition x = f + g n'est pas unique et donc l'image s(x) = f - g ne l'est pas non plus. Du coup, s n'est pas bien définie.
C'est la même chose avec les projections. La projection sur F parallèlement à G est définie par:
p(x) = f
Si la somme n'est pas directe, la projection est mal définie.
On dit que F et G sont en somme directe si l'intersection de F et G ne contient que 0. On peut d'ailleurs remarquer qu'elle contient forcément 0 car F et G sont des espaces vectoriels.
Cette condition est par ailleurs équivalente à la condition suivante:
Pour tout x dans E, il existe un unique f dans F et un unique g dans G tel que x = f + g.
Pour montrer ce truc là, ce n'est pas bien compliqué.
Supposons que la première condition soit vraie.
On suppose que x s'écrit de deux manières différentes: x = f_1 + g_1 = f_2 + g_2
Alors: f_1 - f_2 = g_2 - g_1
Donc f_1 - f_2 appartient à la fois à F et G donc vaut 0. D'où f_1 = f_2.
Et de même, g_1 = g_2.
Supposons que la deuxième condition soit vraie.
On se donne x qui appartient à la fois à F et à G.
Tu sais que x = f + g avec f dans F et g dans G uniques.
Donc x + 0 = f + g.
0 est dans G donc par unicité, g = 0.
Donc: x = f
Mais: 0 + x = f + 0
Le 0 de gauche appartien à F, x appartient à G, f appartient à F et 0 appartient à G.
Par unicité, x = 0.
Ok merci infiniment !!!
Qu'entends-tu par "symétrie ou projection mal définie" ?
Désolé si je paraît aussi curieux ^^ mais j'ai encore quelque questions :
Tu prends
Réciproquement, est-ce que si s vérifie s² = Id, alors s est une symétrie ?
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Quand je dis mal définie, ça veut dire que l'application considérée peut envoyer un élément de son ensemble de définition sur deux images différentes, ce qui n'est pas possible.
Le résultat suivant est vrai et important:
Soit f une application linéaire.
f est une projection si et seulement si f^2 = f.
f est une symétrie si et seulement si f^2 = Id.
Pour te donner un exemple de symétrie, je te propose de te placer dans le plan.
Ici) \oplus Vect((01;))) .
.
Tu as:)) et
et )) .
.
La symétrie sur F parralèllement à G est la symétrie axiale par rapport à l'axe (Ox).
Le résultat suivant est vrai et important:
Soit f une application linéaire.
f est une projection si et seulement si f^2 = f.
f est une symétrie si et seulement si f^2 = Id.
Pour te donner un exemple de symétrie, je te propose de te placer dans le plan.
Ici
Tu as:
La symétrie sur F parralèllement à G est la symétrie axiale par rapport à l'axe (Ox).
egan a écrit:Quand je dis mal définie, ça veut dire que l'application considérée peut envoyer un élément de son ensemble de définition sur deux images différentes, ce qui n'est pas possible.
Le résultat suivant est vrai et important:
Soit f une application linéaire.
f est une projection si et seulement si f^2 = f.
f est une symétrie si et seulement si f^2 = Id.
Pour te donner un exemple de symétrie, je te propose de te placer dans le plan.
Ici.
Tu as:et
.
La symétrie sur F parralèllement à G est la symétrie axiale par rapport à l'axe (Ox).
Merci pour cet exemple :king2:
Quand tu dis f une application linéaire : pourquoi linéaire ?
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
egan a écrit:Parce qu'une symétrie et une projection sont linéaires.
Ok très bien merci encore pour ce coup de pouce :lol2:
Grâce à toi j'ai compris cette notion de symétrie en algèbre linéaire.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Par contre, pdt qu'on y est, je ne comprends pas la notion de projection en algèbre.
Pourrais-tu me l'expliquer comme tu l'as fait avec la symétrie s'il te plait ?
Par contre, pdt qu'on y est, je ne comprends pas la notion de projection en algèbre.
Pourrais-tu me l'expliquer comme tu l'as fait avec la symétrie s'il te plait ?
J'ai essayé de démontrer en détail (pour voir si je comprenais bien) que pour toute symétrie , on a
, on a 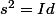 , dites-moi si je me trompe.
, dites-moi si je me trompe.
On se place sur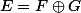 où
où  et
et  sont deux sous-espaces vectoriels d'un même même espace vectoriel
sont deux sous-espaces vectoriels d'un même même espace vectoriel  .
.
On appelle symétrie par rapport à parallèlement à
parallèlement à  l'application linéaire
l'application linéaire 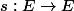 qui à tout
qui à tout \in F\times G, x=f+g) associe
associe =s(f+g)=s(f)+s(g)=f-g) .
.
Par suite,=s(s(x)) =s(f-g)=s(f)-s(g)=f-(-g)=f+g=x) .
.
Ai-je bon ?
J'avoue que j'ai du mal à faire une formulation aussi correcte que complète, en particulier, je ne sais pas si ca se dit ou si c'est bien formulé :
Pourrais-tu me l'expliquer comme tu l'as fait avec la symétrie s'il te plait ?
Par contre, pdt qu'on y est, je ne comprends pas la notion de projection en algèbre.
Pourrais-tu me l'expliquer comme tu l'as fait avec la symétrie s'il te plait ?
J'ai essayé de démontrer en détail (pour voir si je comprenais bien) que pour toute symétrie
On se place sur
On appelle symétrie par rapport à
Par suite,
Ai-je bon ?
J'avoue que j'ai du mal à faire une formulation aussi correcte que complète, en particulier, je ne sais pas si ca se dit ou si c'est bien formulé :
On appelle symétrie par rapport àparallèlement à
l'application linéaire
qui à tout
associe
.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
J'ai essayé de démontrer en détail (pour voir si je comprenais bien) que pour toute symétrie  , on a
, on a 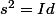 , dites-moi si je me trompe.
, dites-moi si je me trompe.
On se place sur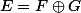 où
où  et
et  sont deux sous-espaces vectoriels d'un même même espace vectoriel
sont deux sous-espaces vectoriels d'un même même espace vectoriel  .
.
On appelle symétrie par rapport à parallèlement à
parallèlement à  l'application linéaire
l'application linéaire 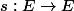 qui à tout
qui à tout \in F\times G, x=f+g) associe
associe =s(f+g)=s(f)+s(g)=f-g) .
.
Par suite,=s(s(x)) =s(f-g)=s(f)-s(g)=f-(-g)=f+g=x) .
.
Ai-je bon ?
J'avoue que j'ai du mal à faire une formulation aussi correcte que complète, en particulier, je ne sais pas si ca se dit ou si c'est bien formulé :
On se place sur
On appelle symétrie par rapport à
Par suite,
Ai-je bon ?
J'avoue que j'ai du mal à faire une formulation aussi correcte que complète, en particulier, je ne sais pas si ca se dit ou si c'est bien formulé :
On appelle symétrie par rapport àparallèlement à
l'application linéaire
qui à tout
associe
.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Ce que tu dis pour les symétries est correct.
Pour les projections:
Soit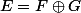 . On appelle p la projection sur F parrallèlement à G.
. On appelle p la projection sur F parrallèlement à G.
Si x est un élément de E, il s'écrit x = f + g et cette décomposition est unique.
Et alors:
p(x) = f
Tu remarqueras que la somme directe te permet de définir p correctement.
Avec cette définition, tu remarques sans trop de problèmes que p^2 = Id.
Pour les projections:
Soit
Si x est un élément de E, il s'écrit x = f + g et cette décomposition est unique.
Et alors:
p(x) = f
Tu remarqueras que la somme directe te permet de définir p correctement.
Avec cette définition, tu remarques sans trop de problèmes que p^2 = Id.
egan a écrit:Ce que tu dis pour les symétries est correct.
Pour les projections:
Soit. On appelle p la projection sur F parrallèlement à G.
Si x est un élément de E, il s'écrit x = f + g et cette décomposition est unique.
Et alors:
p(x) = f
Tu remarqueras que la somme directe te permet de définir p correctement.
Avec cette définition, tu remarques sans trop de problèmes que p^2 = Id.
ok :++:
Merci : grâce à toi j'ai bien compris cette notion de projection et symétrie :+++:
Toutefois, je ne suis pas d'accord avec toi : p²=p et non p²=Id :hum:
J'aurai d'autres questions suite à tt ça :
- Comment montrer qu'une projection p et une symétrie s sont des applications linéaires ?
- Ne pourrais-t-on pas crée une définition similaire à celles de s et p pour une rotation r ?
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Effectivement, je n'ai pas fait attention à ce que j'ai écrit, c'est bien p^2=p.
Tu peux montrer la linéarité de p et s en passant par la décomposition sur la somme directe de F et de G.
La caractérisation des rotations se fait bien sur R^2 et R^3.
Tu trouveras tout ce qu'il faut ici:
http://fr.wikipedia.org/wiki/Matrice_orthogonale
http://fr.wikipedia.org/wiki/Rotation_vectorielle
Commences par le premier lien pour fixer les idées et les définitions.
Si tu as des questions, n'hésites pas.
Tu peux montrer la linéarité de p et s en passant par la décomposition sur la somme directe de F et de G.
La caractérisation des rotations se fait bien sur R^2 et R^3.
Tu trouveras tout ce qu'il faut ici:
http://fr.wikipedia.org/wiki/Matrice_orthogonale
http://fr.wikipedia.org/wiki/Rotation_vectorielle
Commences par le premier lien pour fixer les idées et les définitions.
Si tu as des questions, n'hésites pas.
egan a écrit:Effectivement, je n'ai pas fait attention à ce que j'ai écrit, c'est bien p^2=p.
Tu peux montrer la linéarité de p et s en passant par la décomposition sur la somme directe de F et de G.
La caractérisation des rotations se fait bien sur R^2 et R^3.
Tu trouveras tout ce qu'il faut ici:
http://fr.wikipedia.org/wiki/Matrice_orthogonale
http://fr.wikipedia.org/wiki/Rotation_vectorielle
Commences par le premier lien pour fixer les idées et les définitions.
Si tu as des questions, n'hésites pas.
Ok, c'est très gentil de ta part :++:
Je te tiens au courant de mes questions
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
egan a écrit:
Tu peux montrer la linéarité de p et s en passant par la décomposition sur la somme directe de F et de G.
La caractérisation des rotations se fait bien sur R^2 et R^3.
Dois-je passer par la définition d'une application linéaire ?
-
-
-
idem avec
Quand tu dis "caractérisation", que veux-tu dire exactement ?
Cette caractérisation se fait-elle exclusivement sur
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Oui passe par la définition pour montrer que les symétries et les projections sont linéaires. Tu n'as pas besoin par contre de montrer qu'elles sont nulles en 0. Ca ne sert à rien. Une application linéaire est toujours nulle en 0. Seules les deux dernières conditions correspondent à la vraie définition.
La définition des rotations est très large. On peut déterminer l'ensemble des rotations assez facilement sur R^2 ou R^3. Pour R^n dans le cas général, ça peut se faire mais c'est moins simple.
En tout cas, le résultat sur R^2 et sur R^3 est un truc de cours classique.
La définition des rotations est très large. On peut déterminer l'ensemble des rotations assez facilement sur R^2 ou R^3. Pour R^n dans le cas général, ça peut se faire mais c'est moins simple.
En tout cas, le résultat sur R^2 et sur R^3 est un truc de cours classique.
egan a écrit:Oui passe par la définition pour montrer que les symétries et les projections sont linéaires. Tu n'as pas besoin par contre de montrer qu'elles sont nulles en 0. Ca ne sert à rien. Une application linéaire est toujours nulle en 0. Seules les deux dernières conditions correspondent à la vraie définition.
La définition des rotations est très large. On peut déterminer l'ensemble des rotations assez facilement sur R^2 ou R^3. Pour R^n dans le cas général, ça peut se faire mais c'est moins simple.
En tout cas, le résultat sur R^2 et sur R^3 est un truc de cours classique.
Ok.
PAr contre, je comprends pas pourquoi c'est pas la peine de montrer qu'en 0 ca fait effectivement 0.
Soient
Si
Or
Soit
Ai-je bon ?
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Ta démo est nikel.
J'affirme que une application est linéaire si et seulement si:
 = \lambda f(x) + \mu f(y))
Il est assez simple de montrer que c'est équivalent à:
 = f(x)+f(y))
 = \lambda x)
Si jamais une de ces conditions est vraie, alors:
f(0) = f(0) + f(0)
Donc f(0)=0.
Ces conditions te donnent donc la nullité en 0 donc l'hypothèse de nullité en 0 est redondante donc ne sert à rien.
J'affirme que une application est linéaire si et seulement si:
Il est assez simple de montrer que c'est équivalent à:
Si jamais une de ces conditions est vraie, alors:
f(0) = f(0) + f(0)
Donc f(0)=0.
Ces conditions te donnent donc la nullité en 0 donc l'hypothèse de nullité en 0 est redondante donc ne sert à rien.
Je ne l'ai pas précisé mais le raisonnement est quasiment identique pour s :
=s((f+f')+(g+g'))=f+f'-(g+g')=(f-g)+(f'-g')=s(x)+s(y))
=s(\lambda f +\lambda g )=\lambda f - \lambda g = \lambda (f-g)=\lambda s(x))
As-tu un moyen pour retenir ou retrouver rapidement la forme d'une matrice rotation dans ? Parce que je la retiens, je l'oublie, je la retiens, je l'oublie ...
? Parce que je la retiens, je l'oublie, je la retiens, je l'oublie ...
As-tu un moyen pour retenir ou retrouver rapidement la forme d'une matrice rotation dans
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Je ne l'ai pas précisé mais le raisonnement est quasiment identique pour s :
=s((f+f')+(g+g'))=f+f'-(g+g')=(f-g)+(f'-g')=s(x)+s(y))
=s(\lambda f +\lambda g )=\lambda f - \lambda g = \lambda (f-g)=\lambda s(x))
As-tu un moyen pour retenir ou retrouver rapidement la forme d'une matrice rotation dans ? Parce que je la retiens, je l'oublie, je la retiens, je l'oublie ...
? Parce que je la retiens, je l'oublie, je la retiens, je l'oublie ...
Merci !!!
Ah oui, j'avais oublié qu'on pouvait le montrer avec cette unique égalité !
Merci du rappel :++:
As-tu un moyen pour retenir ou retrouver rapidement la forme d'une matrice rotation dans
egan a écrit:Ta démo est nikel.
J'affirme que une application est linéaire si et seulement si:
Il est assez simple de montrer que c'est équivalent à:
Merci !!!
Ah oui, j'avais oublié qu'on pouvait le montrer avec cette unique égalité !
Merci du rappel :++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
60 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 83 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
