Bonjour à tous,
J'ai besoin de votre aide car je suis très mauvais en maths... Je repasse donc cette matière au rattrapage afin de récupérer des points pour obtenir ma licence.
Je cherche quelqu'un qui pourrais m'expliquer les méthodes à réaliser pour déterminer la divergence et la convergence de séries numériques, par l'exemple si possible, pour une ou plusieurs (si méthode différentes).
J'ai mis un fichier, qui est mon examen 1ere session, afin de vous rendre compte de ce qui est demandé et du niveau de difficulté. Car je pense que notre prof ne nous mets pas des séries trop compliquées.
énoncé au format PDF
Ce n'est pas extrêmement urgent ( j'ai lu la charte... ), mais je passe mon exam lundi, donc j'attends tout de même votre aide avec impatience.
Edit : je possède mes cours, mais par manque de compétences, je n'arrive pas à appliquer une méthode et savoir laquelle appliquée...
Merci d'avance.
Thomas D.
Fac, divergence et séries numériques
7 messages
- Page 1 sur 1
Bonjour,
Pour résoudre un problème de CV/DV de série numérique, il faut appliquer une méthode systématique.
Première question à se poser en face d'une série numérique: est-ce une série à termes positifs (SATP)?
Si oui, alors tu peux appliquer plusieurs méthodes pour montrer la convergence:
-> Montrer que la suite des sommes partielles est majorée
-> Majorer le terme général par le terme général d'une série convergente (de référence), ex Riemann, géométrique...
-> Utiliser les principes de comparaison: soient deux SATP; si
deux SATP; si 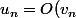) ou si
ou si ) alors la CV de
alors la CV de 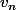 implique la CV de
implique la CV de 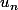 . Et si
. Et si  ~
~  alors
alors  sont de même nature.
sont de même nature.
-> Si la série est à termes strictement positifs, utiliser le critère de d'Alembert version limite ou inégalité (à savoir que le critère version limite donne plus d'informations).
Soit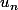 une SATSP.
une SATSP.
Version inégalité:
Si tel que
tel que  alors:
alors:
-si k1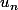 DV
DV
-Si l=1 on ne peut conclure
-> Utiliser le critère de comparaison à une intégrale (rarement utilisé)
Voilà pour les méthodes à appliquer en cas de SATP. Si la série n'est pas à termes positifs, deux cas sont à envisager:
1) La série est alternée (changement de signe à chaque terme), à ce compte-là utiliser le critère spécial des séries alternées: soit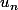 une série alternée. Si la suite
une série alternée. Si la suite ) CV vers 0 EN DECROISSANT, alors la série
CV vers 0 EN DECROISSANT, alors la série 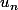 CV et tu as de plus la majoration de la valeur absolue du reste par le premier terme du reste, et le signe de la somme est le signe de
CV et tu as de plus la majoration de la valeur absolue du reste par le premier terme du reste, et le signe de la somme est le signe de  .
.
2) La série est quelconque, on passe par la convergence absolue: montrer la convergence de (comme c'est une SATP on utilise les critères ci-dessus) et on termine en disant que comme la CVA implique la CV,
(comme c'est une SATP on utilise les critères ci-dessus) et on termine en disant que comme la CVA implique la CV, 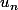 est convergente.
est convergente.
Et pour finir, un critère pour montrer une divergence grossière: une condition nécessaire de convergence de la série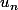 est la convergence vers 0 de la suite
est la convergence vers 0 de la suite ) , donc si la suite ne converge pas vers 0 la série est grossièrement divergente.
, donc si la suite ne converge pas vers 0 la série est grossièrement divergente.
Après, tu peux utiliser une minoration: en minorant le terme général de ta série par le terme général d'une série divergente, tu démontres que ta série diverge.
Pour résoudre un problème de CV/DV de série numérique, il faut appliquer une méthode systématique.
Première question à se poser en face d'une série numérique: est-ce une série à termes positifs (SATP)?
Si oui, alors tu peux appliquer plusieurs méthodes pour montrer la convergence:
-> Montrer que la suite des sommes partielles est majorée
-> Majorer le terme général par le terme général d'une série convergente (de référence), ex Riemann, géométrique...
-> Utiliser les principes de comparaison: soient
-> Si la série est à termes strictement positifs, utiliser le critère de d'Alembert version limite ou inégalité (à savoir que le critère version limite donne plus d'informations).
Soit
Version inégalité:
Si
-si k1
-Si l=1 on ne peut conclure
-> Utiliser le critère de comparaison à une intégrale (rarement utilisé)
Voilà pour les méthodes à appliquer en cas de SATP. Si la série n'est pas à termes positifs, deux cas sont à envisager:
1) La série est alternée (changement de signe à chaque terme), à ce compte-là utiliser le critère spécial des séries alternées: soit
2) La série est quelconque, on passe par la convergence absolue: montrer la convergence de
Et pour finir, un critère pour montrer une divergence grossière: une condition nécessaire de convergence de la série
Après, tu peux utiliser une minoration: en minorant le terme général de ta série par le terme général d'une série divergente, tu démontres que ta série diverge.
Peacekeeper a donné une excellente réponse à ta question et je ne pense pas faire mieux...à part peut-être conseiller de systématiquement regarder à 1ere vue si il y a divergence grossière ou si l'on a affaire à une série entière(dans ce cas le critère de D'Alembert achève souvent l'exo) ou encore comparer avec 1/n² ....si cela ne marche pas on réfléchit et applique les méthodes de PeaceKeeper
newman a écrit:Peacekeeper a donné une excellente réponse à ta question et je ne pense pas faire mieux...à part peut-être conseiller de systématiquement regarder à 1ere vue si il y a divergence grossière ou si l'on a affaire à une série entière(dans ce cas le critère de D'Alembert achève souvent l'exo) ou encore comparer avec 1/n² ....si cela ne marche pas on réfléchit et applique les méthodes de PeaceKeeper
Comparer à 1/n² fait partie des méthodes, comparaison à une série de Riemann d'exposant >1 :lol3:
newman a écrit:oui mais disons que 1/n² c'est ce qu'on fait en première approche de manière un peu naive..il m'est arrivé en DS cette année de comparer avec 1/n^(3/2) voire même encore plus recherché...
Certes, généralement c'est c'est l'exposant 2 qui permet de conclure. Mais bon, il ne faut pas perdre de vue qu'à la base c'est à Riemann qu'on compare. Enfin, tu as raison. :happy3:
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
