Equation fonctionnelle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 29 Mai 2010, 23:07
par Nightmare » 29 Mai 2010, 23:07
Tu as f(x+y)=f(x)f(y)
En dérivant par rapport à x, on obtient f'(x+y)=f'(x)f(y) puis en prenant x=0 : f'(y)=f'(0)f(y) et donc f(y)=exp(f'(0)y).
:happy3:
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 30 Mai 2010, 08:50
par AceVentura » 30 Mai 2010, 08:50
Ok ! Il me reste plus qu'à démontrer qu'il existe un unique
=f'(0))
. Si on avait
>0)
, cela résulte du fait que
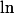
est une bijection de

sur

. Mais comment le prouver ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 30 Mai 2010, 08:54
par Doraki » 30 Mai 2010, 08:54
ln est une bijection de R+* dans R donc pour n'importe quel f'(0) dans R il existe un unique a > 0 tel que ln(a) = f'(0).
Et en fait, a = f(1).
f'(0) > 0 n'a rien à voir là dedans.
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 30 Mai 2010, 08:56
par AceVentura » 30 Mai 2010, 08:56
Euh, en fait non, la surjection suffit !
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 30 Mai 2010, 08:57
par AceVentura » 30 Mai 2010, 08:57
Oui Doraki, je m'en suis rendu compte après !
Avez-vous des applications de ce genre d'équations fonctionnelles ?
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 30 Mai 2010, 09:09
par AceVentura » 30 Mai 2010, 09:09
Le
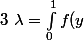dy)
qu'a introduit Nightmare, il est strictement positive car f est continue et strictement positive ? Il n'y a rien d'autres à rajouter comme hypothèse ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 30 Mai 2010, 09:25
par Doraki » 30 Mai 2010, 09:25
oui on a supposé que f ne s'annulait pas, et que f(0) valait 1.
f est continue et strictement positive, donc l'intégrale est > 0.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
