[mpsi] équation fonctionnelle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ghghgh
- Membre Relatif
- Messages: 305
- Enregistré le: 04 Aoû 2006, 15:20
-
 par ghghgh » 16 Nov 2008, 21:50
par ghghgh » 16 Nov 2008, 21:50
Bonsoir,
je ne sais pas résoudre les équations fonctionnelles, et je n'ai pas trop d'idées pour aborder ce problème :
Déterminer les fonctions

continues dans
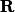
telles que
 = x^2f(x^2))
pour tout nombre réel

non nul.
Comment puis-je m'y prendre ? Une méthode de recherche particulière ? grand merci

-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 16 Nov 2008, 21:56
par ThSQ » 16 Nov 2008, 21:56
Par exemple si 0 < x < 1 f(x) = x² f(x²) = x^.. f(x^...) -> quoi ?
-
ghghgh
- Membre Relatif
- Messages: 305
- Enregistré le: 04 Aoû 2006, 15:20
-
 par ghghgh » 16 Nov 2008, 22:03
par ghghgh » 16 Nov 2008, 22:03
il me semble que f(x^2) = x^6 * f(x^4) dans le cas où 0 < x < 1, j'vérifie encore sur quelques exemples ...
et encore f(x^4) = x^14 * f(x^8) ...
hum, peut-être que c'est
 = x^{4*n-2} * f(x^{2*n}))
edit : non c'est faux, mais il doit exister une relation dans le genre,
pour n = 2, elle est vraie, par contre pour n = 3 elle est fausse,
les exposants doivent sans doute vérifier une suite géométrique :s
et on a encore f(3) = 3^6*f(3^4)
-
JJa
- Membre Relatif
- Messages: 254
- Enregistré le: 06 Mar 2008, 15:52
-
 par JJa » 17 Nov 2008, 08:16
par JJa » 17 Nov 2008, 08:16
Bonjour,
une indication :
faire le changement g(x)=x² f(x)
g(x²)=(x²)²f(x²)=(x^4)f(x²)
f(x²)=f(x)/x²
g(x²)=(x^4)(f(x)/x²) = x²f(x)
g(x²)=g(x)
etc.
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 17 Nov 2008, 09:29
par Maxmau » 17 Nov 2008, 09:29
Bj
En embrayant sur JJa ( g(x²) =g(x) )
La fonction g est paire On peut supposer x > 0 et poser h(t) = g(exp(t))
Doù : h(2t) = h(t) soit encore h(t) = h(t/2)
Doù : h(t/2^n) = h(t) et par continuité ..etc
-
mathelot
 par mathelot » 17 Nov 2008, 09:43
par mathelot » 17 Nov 2008, 09:43
=g(u))
d'où g est constante , vaut g(1).
trop tard, grillé par MaxMau. :we:
-
JJa
- Membre Relatif
- Messages: 254
- Enregistré le: 06 Mar 2008, 15:52
-
 par JJa » 17 Nov 2008, 11:28
par JJa » 17 Nov 2008, 11:28
Attention, le but de mon message précédent n'était pas de vous aiguiller sur le piège qui conduirait à conclure hativement qu'il n'y aurait que l'unique solution g(x)=constante, donc f(x)=c/x².
Bien au contraire, il s'agissait d'une simplification préliminaire facilitant la recherche de la forme générale des solutions f(x), dont il existe une infinité autres que la triviale c/x².
Il est probable que le problème posé à ghghgh n'est pas seulement de trouver cette solution particulière, mais d'exprimer la forme générale des solutions : cela aurait été bien trop facile !
-
phryte
- Membre Irrationnel
- Messages: 1406
- Enregistré le: 05 Juil 2008, 17:09
-
 par phryte » 17 Nov 2008, 11:49
par phryte » 17 Nov 2008, 11:49
Bonjour.
Je propose la fonction
=\frac{k}{x^2})
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 17 Nov 2008, 11:52
par Doraki » 17 Nov 2008, 11:52
Pour x > 0, la suite x^(2^-n) tend vers 1, par continuité de f on peut donc déduire la valeur de f sur R+* à partir de f(1) en itérant la relation :
f(x) = f(x^(1/2))/x = ... = f(x^(2^-n))/(x²)^(1-2^-n) = ... = f(1)/x² (en passant à la limite grâce à la continuité de f)
puis f est paire : f(-x) = x²f(x²) = f(x) = f(1)/x² = f(1)/((-x)²).
Je vois pas comment il peut y avoir d'autres solutions que f(x) = c/x²
-
mathelot
 par mathelot » 17 Nov 2008, 11:52
par mathelot » 17 Nov 2008, 11:52
JJa a écrit:qui conduirait à conclure hativement qu'il n'y aurait que l'unique solution g(x)=constante
=g(x^2))
soit
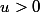
en posant
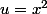
=g(u))
par récurrence:
=g(u))
par continuité,quand l'entier n tend vers l'infini:
g(u)=g(1)
g est donc constante sur

et du coup, l'équation n' a pas de solution continue.
remarque: pour une solution discontinue,
=\frac{1}{x^2})
sur
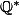
, 0 sinon convient.
-
JJa
- Membre Relatif
- Messages: 254
- Enregistré le: 06 Mar 2008, 15:52
-
 par JJa » 17 Nov 2008, 12:04
par JJa » 17 Nov 2008, 12:04
Il sera instructif de trouver où est l'erreur dans vos raisonnements !
Bon, voici la réponse :
Soit une fonction périodique Per(X) de période p, c'est à dire satisfaisant :
Per(X+p) = Per(X)
(par exemple, une fonction trigonométrique)
Considérons la fonction g(x) = Per( p*ln(x)/ln(2) )
g(2x) = Per( p*ln(2x)/ln(2) )
g(2x) = Per( p*ln(x)/ln(2)+p*ln(2)/ln(2) )
g(2x) = Per( p*ln(x)/ln(2)+p )
g(2x) = Per( p*ln(x)/ln(2) ) , puisque de période p.
donc g(2x) = g(x) ce qui satisfait donc la condition.
Résultat :
f(x) = (1/x²)*Per( p*ln(x)/ln(2) )
Il y a donc une infinité de solutions correspondant à l'infinité des fonctions périodiques.
Note : ceci pour x>0. La réponse s'étend aux x<0 en mettant des valeurs absolues dans le logarithme.
-
mathelot
 par mathelot » 17 Nov 2008, 14:20
par mathelot » 17 Nov 2008, 14:20
JJa a écrit:f(x) = (1/x²)*Per( p*ln(|x|)/ln(2) )
Il y a donc une infinité de solutions correspondant à l'infinité des fonctions périodiques.
il semble que f ne soit pas continue en x=0 :hum:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 17 Nov 2008, 15:01
par Doraki » 17 Nov 2008, 15:01
Euh JJa, tu en étais à g(x²) = g(x), donc je suppose que tu parles de la fonction h(x) = g(exp(t)) dont parlait Maxmau (qui doit bien vérifier h(2x) = h(x))
On veut g continue en 1 (comme f), donc h continue en 0.
Or, Per( p*ln(x)/ln(2)) n'admet pas de limite en 0 donc n'est pas prolongeable, à moins que la fonction périodique choisie soit constante (sinon, Per( p*ln(x)/ln(2)) oscille de plus en plus vite à l'approche de 0).
-
JJa
- Membre Relatif
- Messages: 254
- Enregistré le: 06 Mar 2008, 15:52
-
 par JJa » 17 Nov 2008, 16:13
par JJa » 17 Nov 2008, 16:13
En effet, tout dépend de la façon dont on comprend l'énoncé de la question posée par ghghgh.
- Je l'ai compris ainsi : Déterminer les fonctions f(x) continues dans R ... pour tout nombre réel x non nul.
- Si vous pensez que c'est : Déterminer les fonctions f(x) continues dans R ... pour tout nombre réel x (donc incluant x=0), alors la solution triviale f(x)=c/x² ne convient pas car cette fonction n'est pas continue en x=0. Il est évident que la seule solution serait f(x)=0 quel que soit x. Mais dans ce cas, quel serait l'intérêt de l'exercice ?
C'est pourquoi je privilégie la première interprétation.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 17 Nov 2008, 16:27
par Doraki » 17 Nov 2008, 16:27
JJa, les solutions que tu as obtienues sont des solutions sur R\{-1,0,1}. (tu as du f(x) = P(ln |ln |x||)/x² où P est périodique de période ln(2) au final si je ne m'abuse)
Les seules qui sont prolongeables par continuité en 1 et -1 sont les fonctions x -> c/x² (celles que l'énoncé demande)
Et parmi elles, la seule qui est prolongeable en 0 est la fonction nulle.
-
JJa
- Membre Relatif
- Messages: 254
- Enregistré le: 06 Mar 2008, 15:52
-
 par JJa » 17 Nov 2008, 16:55
par JJa » 17 Nov 2008, 16:55
Doraki,
Premièrement, je ne suis pas d'accord :
Dans f(x)=(1/x²)*Per( X ) avec X=p*ln(abs(x))/ln(2), il s'agit d'une fonction Per(X) périodique de période p (et non pas de période ln(2) )
La fonction est périodique relativement à X, mais bien évidemment, non périodique relativement à x.
Les solutions ne sont pas du tout resteintes sur R{-1,0,1} car cela dépend de la fonction périodique Per(X) que l'on considère : il y a une infinité de possibilités.
Par exemple : avec Per(X)=1/(2+cos(X)) donc de période p=2*pi :
f(x) = (1/x²)/(2+cos( 2*pi*ln(abs(x))/ln(2) ))
Deuxièmement: c'est bien ce que j'ai dit dans mon message précédent, si on impose à f(x) d'être continue en x=0, il n'y a plus que la solution f(x)=0 quel que soit x. Mais dans cette hypothèse, l'exercice est tellement trivial que l'on doute de son intérêt et que l'on doute donc que se soit la bonne façon de comprendre l'énoncé de la question.
Au contraire, si on comprend autrement l'énoncé, comme je l'ai fait, on tombe sur un problème intéressant, avec des solutions non triviales faisant intervenir une réponse très générale avec les fonctions périodiques.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 17 Nov 2008, 17:22
par Doraki » 17 Nov 2008, 17:22
Non il te manque un log dans ta solution.
D'abord, la période de la fonction utilisée n'est pas très importante vu que tu la manipules pour avoir la bonne période.
Je suppose que j'ai pris dès le début une fonction de période ln2 parceque c'est plus simple pour les calculs d'avoir ça que d'avoir à me balader avec Per(p*x/ln2) partout à la place de Per(x)
tu prends f(x) = (1/x²) * P(ln |x|) où P est ln2-périodique (x -> 1/(2+cos(2*pi*x/ln 2)) par exemple)
x²f(x²) = (1/x²) * P( ln |x|²) = (1/x²) * P(2*ln |x|) <> (1/x²) * P(ln |x|) = f(x)
Il faut prendre f(x) = (1/x²) * P(ln |ln |x||).
Alors, ln |ln |x²|| = ln |2*ln |x|| = ln 2 + ln |ln |x||,
et on a bien x²f(x²) = (1/x²) * P(ln2 + ln |ln |x||) =(1/x²) * P(ln |ln |x||) = f(x).
Le log que tu as oublié vient du changement de variable fait par Maxmau pour passer de l'équation g(x²) = g(x) à l'équation g(2x) = g(x), tu es passé de l'une à l'autre par inattention.
Maintenant, ln |ln |x|| n'est pas défini en +-1, or on cherche les solutions qui sont définies et continues en +-1. Pour pouvoir prolonger les solutions, il faut prendre P constante
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 17 Nov 2008, 18:47
par ThSQ » 17 Nov 2008, 18:47
JJa a écrit:En effet, tout dépend de la façon dont on comprend l'énoncé de la question posée par ghghgh.
Tel qu'il est écrit il est non ambigu.
-
JJa
- Membre Relatif
- Messages: 254
- Enregistré le: 06 Mar 2008, 15:52
-
 par JJa » 17 Nov 2008, 19:20
par JJa » 17 Nov 2008, 19:20
Cette fois, je suis d'accord. C'est bien moi qui ai fait erreur en cherchant les solutions de g(2x)=g(x) au lieu de g(x²)=g(x).
De cette erreur, il résulte qu'il faut ln(ln(X)) au lieu de ln(X) et la conséquence est qu'il n'y a plus continuité en -1 et 1.
Par conséquent, il ne reste que la solution f(x)=0 si on exige la continuité en x=0, ou f(x)=c/x² si on n'exige pas cette continuité.
J'applique donc à moi-même ma remarque " chercher l'erreur sera instructif ".
Autant pour moi, ou plutôt au mauvais temps pour moi !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités