Equation fonctionnelle.
je tente de prendre le relai ^^
en fait on a f(x+1) = f(1+1/x)
Si on sait que c'est vrai en x0 : f(x0+1) = f(1+1/x0)
si tu dis que la dérivée est égale en x0, tu admets implicitement que la fonction f se comporte de la même façon au voisinage de x0+1 et au voisinage de 1+1/x0.
Pour voir le comportement à droite en f(x0+1), on regarde f((x0+epsilon)+1).
Or il se trouve que f(1+1/(x0+epsilon)) n'est pas à droite de f(1+1/x0) mais à gauche car 1+1/(x0+epsilon) < 1+1/x0.
Donc en fait rien ne te dit que la valeur à droite de f(x0+1) est la même que celle à droite de f(1+1/x0).
Je sais pas si c'est super clair...
en fait on a f(x+1) = f(1+1/x)
Si on sait que c'est vrai en x0 : f(x0+1) = f(1+1/x0)
si tu dis que la dérivée est égale en x0, tu admets implicitement que la fonction f se comporte de la même façon au voisinage de x0+1 et au voisinage de 1+1/x0.
Pour voir le comportement à droite en f(x0+1), on regarde f((x0+epsilon)+1).
Or il se trouve que f(1+1/(x0+epsilon)) n'est pas à droite de f(1+1/x0) mais à gauche car 1+1/(x0+epsilon) < 1+1/x0.
Donc en fait rien ne te dit que la valeur à droite de f(x0+1) est la même que celle à droite de f(1+1/x0).
Je sais pas si c'est super clair...
Bonjour,
En recherchant un contre-exemple pour B_J je suis retombé sur une fonction qui vérifie la relation=\frac{x^2+x-1}{x-1})
Je l'avais déjà proposée dans le message 21 mais en me plantant dans la transcription :hum:
Cette fonction n'est pas continue en 1 mais elle montre qu'on peut trouver des solutions relativement simples :we:
En recherchant un contre-exemple pour B_J je suis retombé sur une fonction qui vérifie la relation
Je l'avais déjà proposée dans le message 21 mais en me plantant dans la transcription :hum:
Cette fonction n'est pas continue en 1 mais elle montre qu'on peut trouver des solutions relativement simples :we:
Pour ceux qui seraient tentés par le sujet mais qui n'auraient pas le courage de lire l'ensemble de la discussion sur l'autre forum .
On pose:
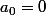 ,
, 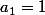 ,
,  .
.
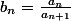 ,
, 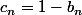 .
.
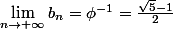 et
et 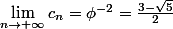 .
.
On définit sur
sur 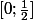 avec les conditions :
avec les conditions :
 est continue sur
est continue sur 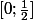 avec
avec  = 0) et
et  = i(\displaystyle{\frac{1}{2}) = k}) .
.
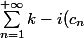 = l}) existe .
existe .
On complète alors sur
sur  de la façon suivante :
de la façon suivante :
 = -i(-x)) si
si 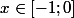 .
.
 = i(x-1)+i(\frac{1-x}{x})+k}) si
si 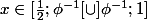 .
.
 = l) .
.
 = i(x^{-1})) si
si 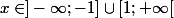 .
.
Il n'y a plus qu'à poser : = i(x-1) + k) pour avoir une solution au problème . Un exemple simple de fonction
pour avoir une solution au problème . Un exemple simple de fonction  qui satisfait les conditions :
qui satisfait les conditions :
 = x) si
si 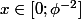
 = \phi^{-2}) si
si 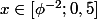 .
.
Et la fonction associée :
associée :  = i(x-1) + \phi^{-2}) .
.
J'ai essayé de joindre l'organigramme pour le calcul de dans ce cas , mais sans résultat .
dans ce cas , mais sans résultat .
Imod
On pose:
On définit
On complète alors
Il n'y a plus qu'à poser :
Et la fonction
J'ai essayé de joindre l'organigramme pour le calcul de
Imod
Imod a écrit:
J'ai essayé de joindre l'organigramme pour le calcul dedans ce cas , mais sans résultat .
Imod
Bonjour et merci
J'ai essayé de voir comment se déroulait ta fonction simple et j'ai une question un peu hors sujet :
As-tu effectivement fait calculer les valeurs de la fonction par une machine ?
J'ai un doute sur la possibilité de la programmer au voisinage de 1,618
As-tu effectivement fait calculer les valeurs de la fonction par une machine ? J'ai un doute sur la possibilité de la programmer au voisinage de 1,618
Après une seconde sur ma TI i(1,618)
Je joins l'organigramme dès que j'ai compris comment joindre un dessin sur ce forum ( désolé je suis novice ) .
Imod
Bonsoir,
Ton organigramme est très clair. Il y a bien une instabilité puisqu'avec le même programme je trouve i(1,618)=0,44921148048 et non 0,4492244633
J'ai représenté le graphe de la fonction ci dessous : attention c'est f et non pas i en zoomant sur les parties sensibles (autour du nb d'or) Elle se comporte un peu comme sin(1/x)

Ton organigramme est très clair. Il y a bien une instabilité puisqu'avec le même programme je trouve i(1,618)=0,44921148048 et non 0,4492244633
J'ai représenté le graphe de la fonction ci dessous : attention c'est f et non pas i en zoomant sur les parties sensibles (autour du nb d'or) Elle se comporte un peu comme sin(1/x)

Merci Alben pour les graphiques qui permettent en effet de mettre le doigt sur les points délicats . Je me demande du coup s'il ne serait pas plus simple d'étudier une fonction  qui ne changerait pas de définition de part et d'autre du point critique
qui ne changerait pas de définition de part et d'autre du point critique 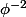 , par exemple :
, par exemple :
=4x \text{ si } x\in[0;\frac{1}{4}]) et
et =1 \text{ si } x\in[\frac{1}{4};\frac{1}{2}]) . Je regarde cela un peu plus en détail .
. Je regarde cela un peu plus en détail .
Imod
Imod
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
