Bonjour!
je suis sur un exercice en ce moment, où dans une question il trouver les fonctions f continues vérifiant une équation avec une intégrale. je n'ai jamais résolu d'équation de cette sorte, j'aurais donc voulu savoir si quelqu'un pouvait m'apporter une méthode.
Merci!
Equation fonctionnelle avec intégrale.
3 messages
- Page 1 sur 1
par dibeteriou » 25 Aoû 2010, 11:49
Un exemple de solution systématique :
En changeant
en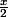 
on trouve :
=2+x\int_0^x f(t)\text{d}t - \int_0^x t f(t)\text{d}t)
Ceci prouve que
est dérivable et que :
=\int_0^x f(t)\text{d}t+xf(x)-xf(x)=\int_0^x f(t)\text{d}t)
on recommence, et on trouve une équation différentielle vérifiée par.
En évaluant les deux équations en un point bien choisi, on trouve une condition initiale : il y a une unique solution, reste à résoudre.
En changeant
Ceci prouve que
on recommence, et on trouve une équation différentielle vérifiée par
En évaluant les deux équations en un point bien choisi, on trouve une condition initiale : il y a une unique solution, reste à résoudre.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Ben314 et 59 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :