Désolé d'avoir peut-être rajouté de la confusion à la confusion, je n'avais pas bien vu que le terme utilisé était "élément maximal".
Ton énoncé du premier post est donc effectivement correct.
Si E est fini, toute partie de P(E) est finie, la relation d'inclusion étant un ordre partiel , son graphe ne contient pas de cycle, et sur toute partie finie, il y a donc au moins un élément maximal (élément contenu dans aucun autre).
Si E est infini, on peut construire une suite
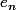
infinie d'éléments de E, distincts deux à deux.
On construit alors la suite
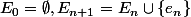
qui n'a donc pas d'élément maximal.
