Dérivabilité exponentielle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
par legeniedesalpages » 13 Nov 2008, 01:03
Bonsoir,
Dans le Rudin "Principes d'analyse mathématique", Il définit l'exponentielle par
=\Bigsum_{n=0}^{\infty} \frac{z^n}{n!})
.
Un peu plus loin il dit que la formule d'addition nous donne
-\exp(z)}{h} = \exp(z)\lim_{h \rightarrow 0} \frac{\exp(h)-1}{h} = \exp(z))
,
la dernière égalité se déduisant immédiatement de la définition de l'exponentielle.
Mais je ne vois pas pourquoi on aurait si facilement cette dernière égalité. De mon côté j'ai trouvé
-1}{h}=\frac{\Bigsum_{n=0}^{\infty} \frac{h^n}{n!}-1}{h}=\Bigsum_{n=1}^{\infty} \frac{h^{n-1}}{n!})
et là je ne vois pas comment montrer que ça tend vers 1 quand
tend vers 0?
Merci pour votre aide.
-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
par fatal_error » 13 Nov 2008, 07:53
salut,
apartir de
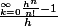
quand n vaut 0, h^n vaut 1 on peut commencer a partir de 1:
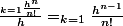
on veut monter que le dernier terme tend vers 1
quand n vaut 1, h^{n-1} vaut 1 (n-1=0)
Du coup
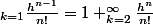
la vie est une fête
-
mathelot
par mathelot » 13 Nov 2008, 08:03
)
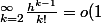en majorant la norme de la série par ||h|| pour h petit.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
