Bonjour les matheux...
Je bute sur une question d'un probleme (qui ne depend d'aucune autre question...):
Montrer que l'ensemble des points à coordonnées rationnelles est dense dans le cercle unité.
J'avoue que cela ne me parait pas naturel mais bon....
Pouvez vous m'aider......
Densité
6 messages
- Page 1 sur 1
Je sais pas, peut être une idée:
On considére l'application définie sur
définie sur  par
par
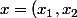 \longrightarrow \frac{x}{||x||^2} = \frac{x}{\sum x_i^2})
C'est une homéomorphie de\}) sur lui-même.
sur lui-même.
Elle transforme la droite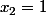 de
de  en
en \}) où
où  est le cercle unité.
est le cercle unité.
La droite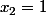 est homéomorphe à
est homéomorphe à  par l'homéomorphisme
par l'homéomorphisme  = (x,1)) .
.
Donc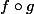 est une homémorphie de
est une homémorphie de  sur
sur \}) .
.
 \subset \mathbb{Q}\times \mathbb{Q}) et
et } = S\setminus\{(0,0)\}) .
.
Donc tout point de\}) est limite d'une suite de points de
est limite d'une suite de points de \cap S\setminus\{(0,0)\}) .
.
D'autre part) est limite de la suite à coefficients rationnels de points de
est limite de la suite à coefficients rationnels de points de  :
: ,(0,0),\cdots)) .
.
Donc tout point de est limite d'une suite de points de
est limite d'une suite de points de  à coefficients rationnels.
à coefficients rationnels.
Sauf erreur.
On considére l'application
C'est une homéomorphie de
Elle transforme la droite
La droite
Donc
Donc tout point de
D'autre part
Donc tout point de
Sauf erreur.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
