Densité
19 messages
- Page 1 sur 1
densité
Bonjour,
Mon intuition me dit que l'ensemble des 2^n/3^m (m et n dans N) est dense dans R+, mais je n'arrive pas à le démontrer.
Quelqu'un a-t-il une idée ?
Merci
Mon intuition me dit que l'ensemble des 2^n/3^m (m et n dans N) est dense dans R+, mais je n'arrive pas à le démontrer.
Quelqu'un a-t-il une idée ?
Merci
Re: densité
C'est bien sûr la bonne idée , on peut aussi prendre m et n dans Z pour utiliser ensuite un résultat connu .
Imod
Imod
Re: densité
Je cherche n et m tels que a<(2^n/3^m)<b, pour a et b arbitraires.
Je passe aux logarithmes, et je dois construire n et m tels que :
ln(a)/mln(2) + ln(3)/ln(2) < m/n < ln(b)/mln(2) + ln(3)/ln(2).
Ce qui me semble faisable, mais je ne vois pas précisément comment.
Merci pour votre aide.
P. S. : quel est donc ce résultat "connu" ?
Je passe aux logarithmes, et je dois construire n et m tels que :
ln(a)/mln(2) + ln(3)/ln(2) < m/n < ln(b)/mln(2) + ln(3)/ln(2).
Ce qui me semble faisable, mais je ne vois pas précisément comment.
Merci pour votre aide.
P. S. : quel est donc ce résultat "connu" ?
Re: densité
Bonjour
Je pense que l'exercice 2 du lien suivant devrait t'éclairer
https://perso.eleves.ens-rennes.fr/peop ... de%20R.pdf
Je pense que l'exercice 2 du lien suivant devrait t'éclairer
https://perso.eleves.ens-rennes.fr/peop ... de%20R.pdf
Re: densité
Merci beaucoup !
Je n'ai pas encore regardé en détail, mais je pense qu'avec ça je vais y arriver.
Je vous tiens au courant.
Paquito.
Je n'ai pas encore regardé en détail, mais je pense qu'avec ça je vais y arriver.
Je vous tiens au courant.
Paquito.
Re: densité
J'ai repris ma recherche sur mon exercice. J'obtiens que l'ensemble des 2^n/3^m est dense dans R*+, pour n et m dans Z. Mais qu'en est-il pour n et m dans N ? Pour ce que je veux en faire, des fréquences musicales, via des divisions de cordes, j'ai besoin que n et m soient positifs.
Merci pour vos idées.
Paquito
Merci pour vos idées.
Paquito
Re: densité
Si  est un réel strictement positif . On cherche des entiers naturels
est un réel strictement positif . On cherche des entiers naturels  et
et  tels que
tels que  soit aussi proche que l’on veut de
soit aussi proche que l’on veut de  . En notant
. En notant 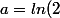 , b=ln(3)) et
et 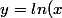) , on est ramené à chercher
, on est ramené à chercher  et
et  pour que
pour que  puisse approcher
puisse approcher  autant qu’on le souhaite . Comme les parties fractionnaires de
autant qu’on le souhaite . Comme les parties fractionnaires de  sont denses dans
sont denses dans  ,
,  peut approcher
peut approcher  à volonté . Il reste à multiplier par b pour conclure .
à volonté . Il reste à multiplier par b pour conclure .
Imod
Imod
Re: densité
Bonjour,
Merci pour ta réponse.
Mais d'une part, y/b pourrait ne pas appartenir à [0,1].
Et d'autre part, où est passé le m ?
Ou quelque chose m'échappe ?
Merci.
Paquito
Merci pour ta réponse.
Mais d'une part, y/b pourrait ne pas appartenir à [0,1].
Et d'autre part, où est passé le m ?
Ou quelque chose m'échappe ?
Merci.
Paquito
Re: densité
Bonjour
Je pense qu'imod a voulu dire que
 peut approcher la partie fractionnaire de
peut approcher la partie fractionnaire de  à volonté
à volonté
Donc
 approche
approche 
ou
 approche
approche 
et en multipliant par b :
 approche
approche 
On aurait donc m=
Mais là se pose la question de savoir si m est positif...
Je pense qu'imod a voulu dire que
Donc
ou
et en multipliant par b :
On aurait donc m=
Mais là se pose la question de savoir si m est positif...
Re: densité
Bonjour,
On passe au logarithme : l'exercice revient à montrer que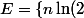-m\ln(3)\mid m,n \in \mathbb N\}) est dense dans
est dense dans  .
.
Le résultat classique sur les sous-groupes additifs de) entraîne que
entraîne que 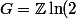+\mathbb Z \ln(3)) est dense dans
est dense dans  , puisque
, puisque /\ln(3)) est irrationnel.
est irrationnel.
Soit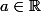 et cherchons à approcher
et cherchons à approcher  par un élément de
par un élément de  à moins de
à moins de 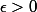 donné. D'après le résultat rappelé plus haut, il existe
donné. D'après le résultat rappelé plus haut, il existe  tel que
tel que )) . Le minimum avec
. Le minimum avec ) sert à s'assurer que
sert à s'assurer que  ou
ou  est dans
est dans  .
.
Supposons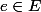 . et choisissons un entier naturel
. et choisissons un entier naturel  tel que
tel que \leq a) . Alors il existe un (unique) entier naturel
. Alors il existe un (unique) entier naturel  tel que
tel que +\ell e\leq a<-k\ln(3)+(\ell+1)e) . On a encadré
. On a encadré  entre deux éléments de
entre deux éléments de  distants de moins de
distants de moins de  , c'est gagné.
, c'est gagné.
Je te laisse gagner dans le cas .
.
On passe au logarithme : l'exercice revient à montrer que
Le résultat classique sur les sous-groupes additifs de
Soit
Supposons
Je te laisse gagner dans le cas
Re: densité
Bonjour,
Je comprends l'idée générale, et le souci de savoir si e appartient à E ou pas.
Mais, mon cerveau faiblissant avec les années, je ne comprends pas la condition e<min(epsilon, ln(2)).
Si ça ne t'embête pas de la détailler un peu...
Merci pour l'intérêt que tu portes à mon problème.
Paquito
Je comprends l'idée générale, et le souci de savoir si e appartient à E ou pas.
Mais, mon cerveau faiblissant avec les années, je ne comprends pas la condition e<min(epsilon, ln(2)).
Si ça ne t'embête pas de la détailler un peu...
Merci pour l'intérêt que tu portes à mon problème.
Paquito
Re: densité
J'ai expliqué que cette condition sert à s'assurer que 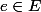 ou
ou  . Supposons que l'on ait eu l'idée farfelue de se donner
. Supposons que l'on ait eu l'idée farfelue de se donner  . Alors on pourrait prendre
. Alors on pourrait prendre  +\ln(3)\in G) , qui est tel que
, qui est tel que  mais qui ne vérifie pas
mais qui ne vérifie pas 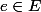 ni
ni  . La condition supplémentaire
. La condition supplémentaire ) impose que dans l'écriture
impose que dans l'écriture  +y\ln(3)) avec
avec  ,
,  et
et  sont forcément de signes opposés.
sont forcément de signes opposés.
Tu n'as pas dit comment gagner dans le cas .
.
Tu n'as pas dit comment gagner dans le cas
Re: densité
Bonjour, de façon à faire avancer le sujet je propose ceci pour le cas "-e dans E" , en espérant ne pas faire trop d'erreurs...
D'abord une remarque sur ce résultat précédent :
Alors il existe un (unique) entier naturel tel que
tel que +\ell e\leq a<-k\ln(3)+(\ell+1)e) .
.
il est obtenu en choisissant égal à la partie entière de
égal à la partie entière de }{e}) qui est positif
qui est positif
comme e>0 on obtient la double inégalité.
Dans l'autre situation, "-e dans E", on choisit cette fois k tel que\geq a)
la partie entière de}{-e}) est positive on la note
est positive on la note  avec
avec  entier naturel
entier naturel
Donc}{-e}<\ell+1)
Comme -e<0 on obtient
-\ell e\geq a>-k\ln(3)-(\ell+1)e)
Les bornes sont bien dans E et leur différence e est inférieure à epsilon.
D'abord une remarque sur ce résultat précédent :
Alors il existe un (unique) entier naturel
il est obtenu en choisissant
comme e>0 on obtient la double inégalité.
Dans l'autre situation, "-e dans E", on choisit cette fois k tel que
la partie entière de
Donc
Comme -e<0 on obtient
Les bornes sont bien dans E et leur différence e est inférieure à epsilon.
Re: densité
Hum catamat !
Comment veux-tu trouver un entier naturel tel que
tel que  \geq a) quand
quand  ?
?
Ce n'est pas difficile à réparer, je te laisse y penser.
Comment veux-tu trouver un entier naturel
Ce n'est pas difficile à réparer, je te laisse y penser.
Re: densité
GaBuZoMeu a écrit:Hum catamat !
Comment veux-tu trouver un entier natureltel que
quand
?
Ce n'est pas difficile à réparer, je te laisse y penser.
Oui merci GaBuZoMeu, après avoir posté je me suis douté qu'il y avait un problème à ce niveau....
Je pense que l'on choisit k entier naturel tel que
Re: densité
Ben voila ...
Je trouve que faire intervenir la partie entière n'éclaircit pas vraiment la démarche.
L'idée est qu'on peut trouver dans un tout petit pas montant ou un tout petit pas descendant. Si on a un petit pas montant, on part d'un élément "évident" de
un tout petit pas montant ou un tout petit pas descendant. Si on a un petit pas montant, on part d'un élément "évident" de  en-dessous de
en-dessous de  et on monte par petits pas en s'arrêtant dès qu'on dépasse
et on monte par petits pas en s'arrêtant dès qu'on dépasse  . Si on a un petit pas descendant, on part d'un élément "évident" de
. Si on a un petit pas descendant, on part d'un élément "évident" de  au-dessus de
au-dessus de  et on descend par petits pas en s'arrêtant dès qu'on passe en dessous de
et on descend par petits pas en s'arrêtant dès qu'on passe en dessous de  . Dans les deux cas, le processus se termine bien par archimédianité.
. Dans les deux cas, le processus se termine bien par archimédianité.
Je trouve que faire intervenir la partie entière n'éclaircit pas vraiment la démarche.
L'idée est qu'on peut trouver dans
Re: densité
Bien chers tous,
Non, je ne me désintéresse pas du problème mais je n'ai pas toujours le temps nécessaire pour m'y consacrer.
De plus, rien ne presse... puisque c'est juste pour le plaisir de (re)faire un peu de mathématiques, sans contraintes.
Je vous remercie chaleureusement pour toutes vos contributions, et vous confirme que je vais y réfléchir dès que possible.
À bientôt donc.
Non, je ne me désintéresse pas du problème mais je n'ai pas toujours le temps nécessaire pour m'y consacrer.
De plus, rien ne presse... puisque c'est juste pour le plaisir de (re)faire un peu de mathématiques, sans contraintes.
Je vous remercie chaleureusement pour toutes vos contributions, et vous confirme que je vais y réfléchir dès que possible.
À bientôt donc.
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
