Salut à tous !
j'ai un petit blocage concernant un exo :
Soit z = exp(i2;)/5)
Posons u = z + z^4 ainsi que v = z² + z^3
Calculer u+v, uv. En déduire u et v.
pour u+v, je trouve 2cos(2;)/5)+2cos(4;)/5)
Le résutat devrait faire -1, mais je ne sais pas si avec ce que j'ai trouvé je peu débouché à ce résultat. Qu'en pensez-vous ?
Complexes
5 messages
- Page 1 sur 1
j'ai entendu parlé de cela, mais je n'ai jamais apprit çà ... Si quelqu'un peut m'expliquer svp. J'ai trouver u + v = 2cos(2/5) + 2cos(4/5). Suis-je dans une impasse, sachant que l'on doit trouver -1 ?
Concernant u.v, j'ai trouver u.v = e(2i/5) + e(4i/5) + e(6i/5) + e(8i/5), suis-je sur la bonne voie ?
Concernant u.v, j'ai trouver u.v = e(2i/5) + e(4i/5) + e(6i/5) + e(8i/5), suis-je sur la bonne voie ?
bonjour,
il s'agit de cinq nombres complexes solutions de
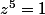
ce sont les racines 5ème de l'unité.
A cause de la progression géométrique

les points ayant ces 5 nombres pour affixes sont les sommets d'un pentagone régulier.
le polynôme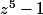 , de la variable complexe z, étant à coefficients réels,sont conjugués deux à deux.
, de la variable complexe z, étant à coefficients réels,sont conjugués deux à deux.
en groupant les racines conjuguées
=2 Re(z_1))
=2 Re(z_2))
pour calculer uv, on utilise la propriété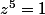
ce qui réduit les exposants des puissances de z: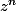 modulo 5.
modulo 5.
 si n et p sont congrus modulo 5.
si n et p sont congrus modulo 5.
il s'agit de cinq nombres complexes solutions de
ce sont les racines 5ème de l'unité.
A cause de la progression géométrique
les points ayant ces 5 nombres pour affixes sont les sommets d'un pentagone régulier.
le polynôme
en groupant les racines conjuguées
pour calculer uv, on utilise la propriété
ce qui réduit les exposants des puissances de z:
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
