Je n'ai aucune idée...
Base orthonormée
30 messages
- Page 1 sur 2 - 1, 2
base orthonormée
Bonsoir, j'aurais besoin d'aide pour trouver une base orthonormée de 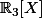 pour le produit scalaire
pour le produit scalaire 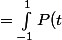 Q(t) dt) .
.
Je n'ai aucune idée...
Je n'ai aucune idée...
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Salut !
Peux-tu me guider, je n'ai jamais pratiquer Gram-Schmidt ...
Peux-tu me guider, je n'ai jamais pratiquer Gram-Schmidt ...
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
||1||²=int(de -1 à1) de 1dx =2 tu prends donc e1=1/rac(2)
tu enlèves la composante selon e1 de X : X-(e1,X)e1 tu normes ton vecteur, c'est e2
tu enlèves les composantes e1,e2 de X² : X²-(e1,X²)e1-(e2,X²)e2 tu normes c'est e3
tu enlèves les composantes e1,e2,e3 de X^3 ...
[procédé d'orthonormalisation de Schmit de la base 1,X,X²,X^3]
tu enlèves la composante selon e1 de X : X-(e1,X)e1 tu normes ton vecteur, c'est e2
tu enlèves les composantes e1,e2 de X² : X²-(e1,X²)e1-(e2,X²)e2 tu normes c'est e3
tu enlèves les composantes e1,e2,e3 de X^3 ...
[procédé d'orthonormalisation de Schmit de la base 1,X,X²,X^3]
jlb a écrit:1||²=2 tu prends donc e1=1/rac(2)
tu enlèves la composante selon e1 de X : X-(e1,X)e1 tu normes ton vecteur, c'est e2
tu enlèves les composantes e1,e2 de X² : X²-(e1,X²)e1-(e2,X²)e2 tu normes c'est e3
tu enlèves les composantes e1,e2,e3 de X^3 ...
[procédé d'orthonormalisation de Schmit de la base 1,X,X²,X^3]
Je ne comprends pas ton début :triste:
Qu'est-ce que "1||²=2" et d'où cela sort-il ?
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Je ne comprends pas ton début :triste:
Qu'est-ce que "1||²=2" et d'où cela sort-il ?
Ah !
En fait :
Mais je ne vois pas d'où sort ton
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Ah donc en fait, si on appelle 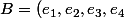=(1,X,X^2,X^3)) la base canonique de
la base canonique de 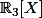 et
et 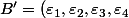) la base orthogonale pour le produit scalaire
la base orthogonale pour le produit scalaire  alors :
alors :
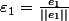 ?
?
D'où le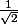 ?
?
D'où le
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Ok, merci !
Par contre, je ne comprends pas bien la suite pour obtenir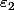 .
.
Par quoi dois-je commencer ?
Ne procéderais-t-on pas comme pour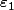 ?
?
On calcule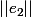 puis on trouve
puis on trouve 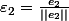 .
.
Par contre, je ne comprends pas bien la suite pour obtenir
Par quoi dois-je commencer ?
Ne procéderais-t-on pas comme pour
On calcule
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
adrien69 a écrit:Non. En fait le truc c'est de te dire que tu te places dans le plan)
Et ensuite tu prends un vecteur temporairetel que
.
Tu résous, ça te donne ta condition sur
et ensuite tu n'as plus qu'à normaliserpour obtenir
Ok, mais j'ai un petit problème :
Donc je trouve a=0, ce qui devrait être impossible, non ?
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
adrien69 a écrit:Tu t'es planté dans ton calcul. Tu as dû oublier la définition deà mon avis.
Ben on a trouvé
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Je ne comprends pas :cry:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
tu as juste: 1 et X sont orthogonaux ( tout comme 1 et X^3) pour ce produit scalaire
donc pour X tu le normes cela suffit! ||pas d'oubli cette fois ! X||²=2/3 d'où e2=rac(3)X/rac(2)
après calcule X²-(e1,X²)e1-(e2,X²)e2 = X²-(e1,X²)e1 car e2 et X² sont orthogonaux ( produit deg impaire) et tu normes pour avoir e3
tu finis avec X^3-(e1,X^3)e1 {ça vaut 0}-(e2,X^3)e2-(e3,x^3)e3 et tu normes, tu as e4
donc pour X tu le normes cela suffit! ||pas d'oubli cette fois ! X||²=2/3 d'où e2=rac(3)X/rac(2)
après calcule X²-(e1,X²)e1-(e2,X²)e2 = X²-(e1,X²)e1 car e2 et X² sont orthogonaux ( produit deg impaire) et tu normes pour avoir e3
tu finis avec X^3-(e1,X^3)e1 {ça vaut 0}-(e2,X^3)e2-(e3,x^3)e3 et tu normes, tu as e4
jlb a écrit:tu as juste 1 et X sont orthogonaux ( tout comme 1 et X^3) pour ce produit scalaire
donc pour X tu le normes cela suffit! ||pas d'oubli cette fois ! X||²=2/3 d'où e2=rac(3)X/rac(2)
après calcule X²-(e1,X²)e1-(e2,X²)e2 = X²-(e1,X²)e1 e2 et X² sont orthogonaux ( produit deg impaire) et tu normes pour avoir e3
Je veux bien normer X mais pourquoi obtiens-tu
Pourquoi normer X ?
J'ai du mal à voir le déroulement du calcul.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
30 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
