Arithmétique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 03 Déc 2008, 17:53
par axiome » 03 Déc 2008, 17:53
Bonsoir à tous,
Voilà, j'ai un exercice d'arithmétique sympathique mais qui me résiste depuis deux jours, si quelqu'un pouvait me donner un coup de pouce, ce serait bien sympa...
Il est court mais quand même coriace... :happy2:
Voilà l'énoncé :
Soit a un entier non nul et m, n des entiers positifs. Montrer que :
=a^{PGCD(m ; n)}-1)
Merci à ceux qui m'aideront.
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 03 Déc 2008, 17:56
par skilveg » 03 Déc 2008, 17:56
Regarde ce qui se passe quand on fait une division euclidienne...
Bonne soirée
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 03 Déc 2008, 18:00
par axiome » 03 Déc 2008, 18:00
Euh, la division euclidienne de quoi par quoi exactement ?
J'avais pensé montrer que
=k*a^{PGCD(m ; n)}-1)
et que
}-1=k'*PGCD(a^m-1 ; a^n-1))
avec k et k' entiers relatifs.
Mais je n'ai pas abouti...
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 03 Déc 2008, 18:14
par ffpower » 03 Déc 2008, 18:14
Une division euclidienne de m par n(si m>n)
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 03 Déc 2008, 18:43
par ThSQ » 03 Déc 2008, 18:43
Ca peut se fait comme que l'algorithme d'Euclide pour calculer les pgcd aussi si on veut :
=PGCD(a^{m-n}-1, a^n-1))
si m > n
D'ailleurs on a aussi :
= X^{pgcd(m,n)} - 1)
comme polynômes.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 03 Déc 2008, 19:36
par leon1789 » 03 Déc 2008, 19:36
skilveg a écrit:Regarde ce qui se passe quand on fait une division euclidienne...
Bonne soirée
ben je fais ça très différemment, avec du calcul modulaire, c'est quasi-immédiat :
soit d=pgcd(m,n)
Modulo a^d -1, on a a^d = 1 donc a^n = ... et a^m = ...
donc a^d -1 divise ...
Soit k un diviseur commun à a^n - 1 et a^m - 1
Alors modulo k, on a a^n = 1 et a^m = 1
Od d = un +vm (Bezout) donc a^d = ...
donc k divise ...
conclusion : a^d -1 est donc...

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 03 Déc 2008, 19:37
par leon1789 » 03 Déc 2008, 19:37
ThSQ a écrit:Ca peut se fait comme que l'algorithme d'Euclide pour calculer les pgcd aussi si on veut :
Algo d'Euclide tu dis ? enfin, ce que j'arrive à déchiffrer :zen:
ThSQ a écrit:D'ailleurs on a aussi :
= X^{pgcd(m,n)} - 1)
comme polynômes.
On a aussi

pour tout élément a d'un anneau commutatif.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 03 Déc 2008, 19:54
par ThSQ » 03 Déc 2008, 19:54
leon1789 a écrit:Algo d'Euclide tu dis ?
Oui, ca faire Euclide peut calculer.
leon1789 a écrit:un anneau commutatif.
et unitaire ... :zen:

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 03 Déc 2008, 20:25
par leon1789 » 03 Déc 2008, 20:25
:id:
ThSQ a écrit:Oui, ca faire Euclide peut calculer.
Tu t'es
lu quand tu as bu ? :beer:
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 04 Déc 2008, 13:48
par axiome » 04 Déc 2008, 13:48
Merci beaucoup à vous tous pour votre aide, j'ai résolu mon problème... :++:
Je suis quand même un peu effrayé par le niveau générale : quand je vois en combien de temps vous résolvez mes problèmes qui me bloquent depuis 2 jours, ça me complexe... :cry:
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 07 Déc 2008, 13:50
par axiome » 07 Déc 2008, 13:50
leon1789 a écrit:Od d = un +vm (Bezout) donc a^d = ...
Salut, juste une petite question encore SVP.
C'est ce donc qui me pose problème.
Pour montrer que
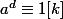
, tu fais :
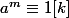
donc
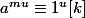
donc
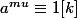
De même, tu démontre que :
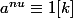
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 07 Déc 2008, 14:00
par axiome » 07 Déc 2008, 14:00
leon1789 a écrit:Od d = un +vm (Bezout) donc a^d = ...
Salut, juste une petite question encore SVP.
C'est ce donc qui me pose problème.
Pour montrer que
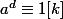
, tu fais :
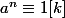
donc
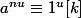
donc
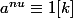
De même, tu démontres que :
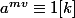
Conclusion :
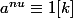
et
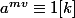
donc
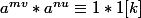
donc
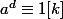
C'est bien cela ?
Parce qu'en fait, ce qui m'embête dans cette démonstration, c'est d'élever à la puissance u et à la puissance v le
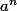
et le
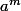
.
Ce sont des entiers relatifs, alors ça m'embête un peu.
Je dois faire erreur quelque part, pourrais-tu détailler un peu plus.
Merci.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 07 Déc 2008, 14:08
par Doraki » 07 Déc 2008, 14:08
Si par exemple, nu est négatif,
tu peux rester dans les exposants positif en disant que
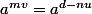
, donc en passant modulo k,
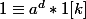
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 07 Déc 2008, 14:26
par axiome » 07 Déc 2008, 14:26
Oki, pas bête !
Merci de la précision.
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 07 Déc 2008, 15:29
par axiome » 07 Déc 2008, 15:29
Euh, encore un détail (le dernier j'espère :marteau:)
J'ai donc démontré :
=k*a^{PGCD(m ; n)}-1)
et
}-1=k*PGCD(a^m-1 ; a^n-1))
Mais de ça, j'en déduis seulement que
}-1)
et
)
sont soit égaux soit opposés puisque a est un entier relatif par hypothèse...
Il faudrait donc que je démontre que
}-1)
est positif...
Et je bloque...
Si qqn a une idée...
Merci.
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 07 Déc 2008, 15:56
par axiome » 07 Déc 2008, 15:56
Encore un détail (le dernier j'espère :marteau:)
J'ai donc démontré :
)
est divisible par
}-1)
et
}-1)
est divisible par
)
Le problème, comme a est un entier relatif, est que je peux seulement en déduire que ces deux nombres sont soit égaux soit opposés...
Je sais déjà que
)
est positif puisque c'est un PGCD.
Il faudrait donc encore démontrer que
}-1)
est positif.
Et là, je bloque...
Un dernier coup de pouce, ce serait sympa... :we:
Merci.
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 07 Déc 2008, 16:01
par ffpower » 07 Déc 2008, 16:01
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 07 Déc 2008, 16:04
par axiome » 07 Déc 2008, 16:04
ffpower a écrit:}-1\geq a-1\geq 0)
Merci de la réponse.
Euh, c'est valable pour a entier relatif ?
Pourrais-tu détailler un peu plus SVP ? Ce n'est pas si évident pour moi... :marteau:
Merci.
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 07 Déc 2008, 16:31
par ffpower » 07 Déc 2008, 16:31
C est évidemment pas vrai si a est negatif..
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 07 Déc 2008, 16:34
par axiome » 07 Déc 2008, 16:34
ffpower a écrit:C est évidemment pas vrai si a est negatif..
C'est justement ça qui m'embête bien...
Parce que ma démo, j'ai presque fini, sauf que je n'arrive pas à prouver l'égalité des deux nombres... :marteau:
Enfin, j'y suis presque : je sais qu'ils sont égaux ou opposés mais après pour démontrer qu'ils sont de même signe (signe positif) pour prouver l'égalité, ce n'est pas évident...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
