Applications
15 messages
- Page 1 sur 1
Applications
Bonjour,
Je commence un chapitre sur les applications et je bloque sur un exo.
On a f une application de E vers E tq fofof=f
Et il faut montrer que f est injective si et seulement si elle est injective
Je commence un chapitre sur les applications et je bloque sur un exo.
On a f une application de E vers E tq fofof=f
Et il faut montrer que f est injective si et seulement si elle est injective
Re: Applications
seulement si f est surjective ?
Modifié en dernier par mathelot le 30 Nov 2021, 18:03, modifié 1 fois.
Re: Applications
f est injective si et seulement f est injective
c'est bouleversant ce truc, non?
c'est bouleversant ce truc, non?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Applications
mathelot a écrit:on suppose f injective.
Que peut on dire de?
je réitère ma question..
Re: Applications
bonsoir,
(x)=f(x))
supposons f injective
on en déduit alors
(x)=x)
d'où
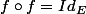
f est donc bijective et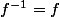
réciproquement, f bijective implique f injective.
Par contre, je n'ai pas sû montrer que "f surjective" implique "f injective"
supposons f injective
on en déduit alors
d'où
f est donc bijective et
réciproquement, f bijective implique f injective.
Par contre, je n'ai pas sû montrer que "f surjective" implique "f injective"
Re: Applications
Bonjour
J'avais trouvé cela :
Soit f surjective et a, b éléments de E tels que f(a)=f(b)
Il faut démontrer que a=b.
Puisque f est surjective il existe a' dans E tel que f(a')=a et a" dans E tel que f(a")=a'
De même on a b' et b" dans E tels que f(b')=b et f(b")=b'
On a donc a=fof(a") et b=fof(b")
Or f(a)=f(b) donc fofof(a")=fofof(b") donc d'après la propriété de f on a f(a")=f(b") c'est à dire a'=b'
donc leurs images par f sont égales : f(a')=f(b') c'est à dire a=b.
J'avais trouvé cela :
Soit f surjective et a, b éléments de E tels que f(a)=f(b)
Il faut démontrer que a=b.
Puisque f est surjective il existe a' dans E tel que f(a')=a et a" dans E tel que f(a")=a'
De même on a b' et b" dans E tels que f(b')=b et f(b")=b'
On a donc a=fof(a") et b=fof(b")
Or f(a)=f(b) donc fofof(a")=fofof(b") donc d'après la propriété de f on a f(a")=f(b") c'est à dire a'=b'
donc leurs images par f sont égales : f(a')=f(b') c'est à dire a=b.
Re: Applications
Salut,
Si f est surjective alors TOUT y s'écrit f (x) et on a fof(y)=fofof(x)=f(x)=y donc fof=Id.
Et le fait que dans les deux cas on a fofof=f => fof=Id peut aussi se voir modulo de savoir (et c'est évident) que :
- f injection => f simplifiable à gauche, c'est à dire que, pour toute fonction g et h, si fog=foh alors g=h.
- f surjective => f simplifiable à droite : si gof=hof alors g=h.
C'est la même chose :mathelot a écrit:Par contre, je n'ai pas sû montrer que "f surjective" implique "f injective"
Si f est surjective alors TOUT y s'écrit f (x) et on a fof(y)=fofof(x)=f(x)=y donc fof=Id.
Et le fait que dans les deux cas on a fofof=f => fof=Id peut aussi se voir modulo de savoir (et c'est évident) que :
- f injection => f simplifiable à gauche, c'est à dire que, pour toute fonction g et h, si fog=foh alors g=h.
- f surjective => f simplifiable à droite : si gof=hof alors g=h.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Applications
Merci,Ben.
Cette classe de fonctions vérifiant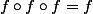 n'est pas vide:
n'est pas vide:
Avec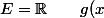=-x+k) (k constante réelle) et
(k constante réelle) et =k) sont des éléments de cette classe.
sont des éléments de cette classe.
Cette classe de fonctions vérifiant
Avec
Re: Applications
Oui, et ta fonction vérifie en fait fof=Id.
Mais peut-tu trouver une fonction de R dans R vérifiant fofof=f mais pas fof=Id ?
Mais peut-tu trouver une fonction de R dans R vérifiant fofof=f mais pas fof=Id ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Applications
Ben314 a écrit:Oui, et ta fonction vérifie en fait fof=Id.
Mais peut-tu trouver une fonction de R dans R vérifiant fofof=f mais pas fof=Id ?
f=constante
Re: Applications
Oui, et on peut mélanger les deux idées, par exemple avec f(x)=1 pour x<0, f(x)=1-x entre 0 et 1 puis f(x)=0 pour x>1.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

