Caractérisation d'applications
49 messages
- Page 2 sur 3 - 1, 2, 3
Je fais surement une erreur quelquepart
1)
Supposons que pour tout a il existe g telle que f=g+a.Id soit solution de l'équation.
Alors(x^{2}+y^{2})=(g+a.Id)^{2}(x)+(g+a.Id)^{2}(y))
+a(x^{2}+y^{2})=g^{2}(x)+g^{2}(y)+2a(g(x)+g(y))+a^{2}(x^{2}+y^{2}))
=g^{2}(x)+g^{2}(y)+2a(g(x)+g(y))+a(a-1)(x^{2}+y^{2})) (*)
(*)
De ce fait, on peut affirmer que g(0)=0. (**)
2)Or si u et v sont deux applications (non identiquement nulles !!!!) solutions de l'équation alors (u+v) n'est pas solution puisque
(x^{2}+y^{2})=u^{2}(x)+u^{2}(y)+v^{2}(x)+v^{2}(y)\neq (u+v)^{2}(x)+(u+v)^{2}(y))
3)Revenons au 1). f et -aId sont solutions. Donc g n'est pas solution ou identiquement nulle.
Le dauxième cas n'est pas interressant. Supposons g non nulle et donc non solution de l'equation, alors dans l'équation (*), il faut que pour tout x et y :
+g(y)\neq \frac{1-a}{2}(x^{2}+y^{2})) . Or pour x=0 et y=0 ceci nous donne
. Or pour x=0 et y=0 ceci nous donne \neq 0) ce qui contredit (**).
ce qui contredit (**).
Donc si une telle fonction g existe, elle est nulle et l'ensemble des solutions sont les fonctions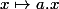
Et en fait, c'est le resultat qui me semble bizzarre
1)
Supposons que pour tout a il existe g telle que f=g+a.Id soit solution de l'équation.
Alors
De ce fait, on peut affirmer que g(0)=0. (**)
2)Or si u et v sont deux applications (non identiquement nulles !!!!) solutions de l'équation alors (u+v) n'est pas solution puisque
3)Revenons au 1). f et -aId sont solutions. Donc g n'est pas solution ou identiquement nulle.
Le dauxième cas n'est pas interressant. Supposons g non nulle et donc non solution de l'equation, alors dans l'équation (*), il faut que pour tout x et y :
Donc si une telle fonction g existe, elle est nulle et l'ensemble des solutions sont les fonctions
Et en fait, c'est le resultat qui me semble bizzarre
thomasg a écrit:Après un peu de réflexion je crois avoir trouvé ton erreur xunil
on a f(x²)=2f(x)² et non f(x²)=2f(x²) comme tu l'écris.
On est donc presque reparti à 0:
deux fonctions constantes sont solution.
continuité en 0+.
toutes mes excuses pour cette bourde... Je ferais plus attention dans mes prochains posts.
Je corrige mon erreur:
on a:
pour tout x dans R+,
Ce qui complique la suite de la piste que j'exploitais...
fahr451 a écrit:est ce si clair la continuité en 0 ?
il faut le résultat a priori pour toute suite x(n) de limite 0 et non pas seulement pour les suites x/2^n
f(x^2) = f(x)^2 + f(0)^2 = f(x)^2 donne f positive sur R +
puis f(x^2 +y^2) - f(x^2) = f(y)^2>=0 donne f croissante sur R +
donc f a une limite en 0+ qui vaut donc f(0)d'après ce qui précède
et la continuité à droite en 0
la dérivabilité à droite en 0 n 'est pas acquise hélas
Très instructif !
Car, autre point intéressant: Soit f(1/2)=0, soit f(1/2)=1/2
(meme raisonnement que 0: f(1/2)=f(1/2²+1/2²)=f(1/2)²+f(1/2)²=2f(1/2)² ...)
Or, Fahr a montré la croissance.
Le couple {(0;1/2);(1/2;0)} est d'ores et déjà impossible
Le couple {(0;1/2);(1/2;1/2)} est possible si f(x)=1/2 sur tout le segment [0;1/2]
Le couple {(0;0);(1/2;0)} est possible si f(x)=0 sur tout le segment [0;1/2]
Le couple {(0;0);(1/2;1/2)} est à l'étude :id:
Je pense avoir résolu l'exercie en supposant la fonction continue. (Et honnètement, il est très rare de pouvoir résoudre une équation fonctionnelle sans supposer la continuité...)
Première étape. Montrons que f est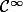 , là où elle est non nulle.
, là où elle est non nulle.
Soit\in(\mathbb{R}^*_{+})^2) , avec
, avec 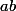 .
.
\in\mathbb{R}_+^2, f(x+y^2)=f(sqrt{x})^2+f(y)^2) .
.
Donc - f(sqrt{x})^2) d x = (b-a)f(y)^2)
Ordx = \int_{a+y^2}^{b+y^2} f(u) du)
On note^2 dx) et F une primitive sur
et F une primitive sur  de
de ) .
.
Si f est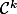 , alors F est
, alors F est 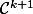 , sur
, sur 
On a alorsf(y)^2 = F(b+y^2) - F(a+y^2) - A) .
. 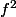 est bien
est bien 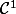 .
.
Pour s'assurer que la racine de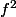 est aussi
est aussi 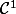 , là où f ne s'annulle pas.
, là où f ne s'annulle pas.
Donc f est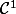 sur
sur 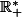 . L'intervalle est ouvert à gauche car on prend la racine et f peut s'annuler en 0.
. L'intervalle est ouvert à gauche car on prend la racine et f peut s'annuler en 0.
Par récurrence, f est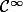 sur
sur 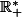 .
.
Seconde étape. On montre que f est en fait affine.
Comme f est dérivable, on peut dériver !
Par rapport à x :\in \mathbb{R}^*_+^2, 2xf'(x^2+y^2)=2f'(x)f(x)) .
.
Donc\in (\mathbb{R}^*_+)^2, f'(x^2+y^2)= \frac{f'(x)f(x)}{x})
En dérivant par rapport à y,\in (\mathbb{R}^*_+)^2, f''(x^2+y^2)=0) .
.
 = 0) .
.
Troisième étape. Synthèse.
f est affine sur .
. \in\mathbb{R}^2, \forall (x,y)\in \mathbb{R}_+^2, f(x) = \alpha x + b) .
.
Or\in\mathbb{R}^2_+, f(x^2+y^2)=f(x)^2+f(y)^2) .
.
Donc\in \mathbb{R}_+^2, \alpha ( x^2 + y^2 ) + \beta = \alpha^2(x^2+y^2) + 2\alpha\beta(x+y) + 2\beta^2) .
.
Comme c'est valable pour un infinité de réels , on a (identification d'un polynôme) :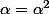 ,
, 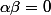 et
et 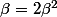 .
.
Donc \in \{ (0;0), (1;0), (0;1/2) \})
Conclusion
Si f est continue, alors f est l'une des trois applications suivantes : la fonction nulle, la fonction constante de valeur 1/2, la fonction identité.
(J'espère qu'il n'y a pas trop de fautes.)
Première étape. Montrons que f est
Soit
Donc
Or
On note
Si f est
On a alors
Pour s'assurer que la racine de
- 1er cas.
Alors.
- 2nd cas.
Supposons que.
Comme f(0)=0, on a
Et on a aussi
Ces deux relations permettent de cronstuire quelque soit c, une suitetendant vers
telle que
.
Supposons que. Alors
.
Donc si f est non nulle, elle ne s'annulle que en 0.
Donc f est
Par récurrence, f est
Seconde étape. On montre que f est en fait affine.
Comme f est dérivable, on peut dériver !
Par rapport à x :
Donc
En dérivant par rapport à y,
Troisième étape. Synthèse.
f est affine sur
Or
Donc
Comme c'est valable pour un infinité de réels , on a (identification d'un polynôme) :
Donc
Conclusion
Si f est continue, alors f est l'une des trois applications suivantes : la fonction nulle, la fonction constante de valeur 1/2, la fonction identité.
(J'espère qu'il n'y a pas trop de fautes.)
Si on suppose que f est continue, alors j'ai une piste:
pour tout x dans R+,=2f^2(\sqrt{\frac{x}{2}})=...=2^{2^n-1}f^{2^n}\left(\frac{x^{\frac{1}{2^n}}}{2^{1-\frac{1}{2^n}}}\right)=2^{2^n-1}\exp[2^nln(f\left(\frac{x^{\frac{1}{2^n}}}{2^{1-\frac{1}{2^n}}}\right)])
cf mon post précédent (et la formule est correcte cette fois, démo par récurrence ).
Or( si f est continue)=f(\frac{1}{2}))
Donc]=\lim_{n \to +\infty}2^{2^n-1}\exp[2^nln(f(\frac{1}{2})])
donc, pour tout x,=\lim_{n \to +\infty}2^{2^n-1}\exp[2^nln(f(\frac{1}{2})]=cste) car f est définie en x.
car f est définie en x.
Or, les seules constantes qui répondent au pb sont 0 et 1/2.
Bon, il y a manifestement un gros pb: où est passé le cas de la fonction identité dans ce raisonnement ?
Et puis, le passage à]) pose un pb de définition: il faut que
pose un pb de définition: il faut que ) soit tjs défini , et donc
soit tjs défini , et donc) soit différent de 0
soit différent de 0
pour tout x dans R+,
cf mon post précédent (et la formule est correcte cette fois, démo par récurrence ).
Or( si f est continue)
Donc
donc, pour tout x,
Or, les seules constantes qui répondent au pb sont 0 et 1/2.
Bon, il y a manifestement un gros pb: où est passé le cas de la fonction identité dans ce raisonnement ?
Et puis, le passage à
C'est ta façon de passer à la limite qui est fausse. Tu avait déjà fait l'erreur ici, dans un cas plus simple :
Tu ne peut pas passer à la limite sur une seule partie de ton expression.
Par exemple :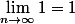 .
.
Or, selon ta méthode,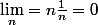 car
car 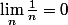 ...
...
J'essaie de trouver une rustine pour ma première étape. En fait, il suffirait de montrer que f est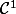 ...
...
xunil a écrit:Donc si f est continue à droite en 0, on a donc pour tout x positif,
et donc comme, on a nécessairement pour tout x de R+ par passage à la limite en n,
Tu ne peut pas passer à la limite sur une seule partie de ton expression.
Par exemple :
Or, selon ta méthode,
J'essaie de trouver une rustine pour ma première étape. En fait, il suffirait de montrer que f est
Ça me parait bien compliqué de passer par les dérivées.
Je reprends mon raisonnement:
f(x²+y²)=f²(x)+f²(y)>0 donc f(z)>0 quand z est dans R+
f(x²+y²)-f²(x)=f²(y)>0 donc f est croissante sur R+
f(0)=f(0²+0²)=f²(0)+f²(0)=2f²(0) donc f(0)=0 OU f(0)=1/2
En résumé, pour que la condition initiale soit respectée, il est nécessaire que f soit la fonction nulle OU la fonction constante 1/2 OU la fonction identité.
Je vous laisse démontrer le côté suffisant.
ok?
Je reprends mon raisonnement:
f(x²+y²)=f²(x)+f²(y)>0 donc f(z)>0 quand z est dans R+
f(x²+y²)-f²(x)=f²(y)>0 donc f est croissante sur R+
f(0)=f(0²+0²)=f²(0)+f²(0)=2f²(0) donc f(0)=0 OU f(0)=1/2
- f(0)=1/2
f(1)=f(1²+0²)=f²(1)+f²(0)=f²(1)+1/4
donc f²(1)-f(1)+1/4=0
donc (f(1)-1/2)²=0
donc f(1)=1/2
f(2)=f(1²+1²)=f²(1)+f²(1)=1/4+1/4 = 1/2
f(8)=f(2²+2²)=f²(2)+f²(2)=1/4+1/4 = 1/2
etc ....
Quelque soit x appartenant à R+, il existe un entier naturel n supérieur à x tel que f(n)=1/2
Comme la fonction f est croissante sur R+, f(x)=1/2
Si f(0)=1/2, quelque soit x appartenant à R+, f(x)=1/2
. - f(0)=0
(f(x)+f(y))² = f²(x)+f²(y)+2f(x)f(y) = f(x²+y²) + 2f(x)f(y) donc f²(x) = (f(x+f(0))²=f(x²)+0=f(x²)
(on peut donc "rentrer ou sortir" le carré à loisir)
De même, f(x²+y²)=f²(x)+f²(y)=f(x²)+f(y²)
(on peut toujours dire que f d'une somme est la somme des f appliquée a chacun)
f(1)=f(1²+0²)=f²(1)+f²(0)=f²(1) donc f(1)=0 OU f(1)=1- f(1)=0
on a donc f(x)=0 quelque soit x appartenant à [0;1]
Tout réel positif se décompose comme la somme de réels entre 0 et 1
donc si f(0)=0 et f(1)=0 alors f(x)=0 quelque soit x appartenant à R+ - f(1)=1
Là, ça se complique un tantinet. Nous n'avons encore rien découvert sur le comportement entre ces valeurs particulières. Décomposer le réel positif en une somme de réels entre 0 et 1 n'a donc pas encore d'intérêt.
Cependant, on note ceci:
f(2)=f(1+1)=f(1)+f(1)=1+1=2
f(3)=f(2+1)=f(2)+f(1)=2+1=3
etc ...
f(1/2)=f(1)/2=1/2 (car 2f(x)=f(x)+f(x)=f(x+x)=f(2x) )
f(1/2^n)=f(1)/2^n=1/2^n avec n entier naturel
Autrement dit, si on peut écrire le réel en base 2 (décomposition en somme de multiple de 1/2^n), alors f appliquée au réel donne ce réel.
on peut démontrer que
si f(0)=0 et f(1)=1, alors f est donc la fonction identité sur R+.
- f(1)=0
En résumé, pour que la condition initiale soit respectée, il est nécessaire que f soit la fonction nulle OU la fonction constante 1/2 OU la fonction identité.
Je vous laisse démontrer le côté suffisant.
ok?
Je suis d'accord avec ta méthode ! (Bien qu'elle mériterait un peu plus de détails. Tu prétend notamment pouvoir montrer la continuité...)
Quant à l'idée de dérivée, elle est non seulement très naturelle (se ramener à une équation différentielle permet d'utiliser une très large palette d'outils) mais aussi simple. C'est montrer la dérivabilité qui est pénible. Mais là encore la méthode est connue et reconnue donc naturelle.
Pour ceux que ça intéresse, le même principe s'applique à l'équation fonctionnelle suivante :
 \\<br />\forall (x,y)\in\mathbb{R}^2, f(x+y)+f(x-y) = 2f(x)f(y))
Quand c'est dérivable c'est facile, mais ça ne l'est pas a priori. Il faut montrer la dérivabilité. On peut appliquer la méthode que j'ai présenté tout à l'heure : passer par un intégration.
Quant à l'idée de dérivée, elle est non seulement très naturelle (se ramener à une équation différentielle permet d'utiliser une très large palette d'outils) mais aussi simple. C'est montrer la dérivabilité qui est pénible. Mais là encore la méthode est connue et reconnue donc naturelle.
Pour ceux que ça intéresse, le même principe s'applique à l'équation fonctionnelle suivante :
Quand c'est dérivable c'est facile, mais ça ne l'est pas a priori. Il faut montrer la dérivabilité. On peut appliquer la méthode que j'ai présenté tout à l'heure : passer par un intégration.
49 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
