2102 résultats trouvés
Revenir à la recherche avancée
Re: [MODIFICATION] Question dans l'arithmethiques
Salut !! c'est une modification et clarification d'une question que j'ai déjà poser. Les Données : P_{n}=[k\in [[0;n-1]]/pgdc(k,n)=1] f est une application de P_{n} vers P_{n} où l'image de k est f(k) où : f(k) est le reste de la division euclidienne de ak sur n où n>1 et a\in IN^{*...
- 07 Mar 2019, 01:35
- Forum: ✎✎ Lycée
- Sujet: [MODIFICATION] Question dans l'arithmethiques
- Réponses: 1
- Vues: 565
Re: petite question svp
Tu peux créer une fonction F qui va de P_n dans Q_n qui a associe à chaque k de P_n , f(k) dans Q_n . * Tu peux montrer que F est bijective (injective qui surjective) => Card(P_n) = Card(Q_n) * Tu peux montrer que Q_n C P_n ainsi Q_n = P_n le produit des f(k) n'est autre que le produit des k...
- 05 Mar 2019, 18:20
- Forum: ✎✎ Lycée
- Sujet: petite question svp
- Réponses: 6
- Vues: 841
Re: Démonstration dans Z svp
Commence par montrer un sens, puis l'autre. De gauche à droit: par absurde: quel implication a-t-on si p divisait k ou q divisait k? L'autre sens: pour montrer P => Q, on montrera que nonQ => nonP: si pgcd(k, n) = d > 1, alors d/k et d/n, right? or si d divise n = pq alors d divise q ou d divise p c...
- 05 Mar 2019, 13:42
- Forum: ✎✎ Lycée
- Sujet: Démonstration dans Z svp
- Réponses: 5
- Vues: 549
Re: petite question svp
Non mais tu pourras utiliser mon astuce pour chercher ta solution.
- 28 Fév 2019, 20:59
- Forum: ✎✎ Lycée
- Sujet: petite question svp
- Réponses: 6
- Vues: 841
Re: Arithmétique
Bonjour,
Tu peux me rappeler comment tu résous une equation de second degrés en general stp? Ca sera ton point de départ.
Tu peux me rappeler comment tu résous une equation de second degrés en general stp? Ca sera ton point de départ.
- 28 Fév 2019, 10:30
- Forum: ✎✎ Lycée
- Sujet: Arithmétique
- Réponses: 5
- Vues: 525
Re: Démonstration dans Z svp
zerow2001 a écrit:c'est là ou je bloque, est ce qu'on peut conclure que a^d est congru à b[n] parce qu'on a (nk+a)^d est congru à a^[n] et on sait que (nk+a)^d est congru à b [n] ?
Yes, le modulo est transitif
- 27 Fév 2019, 09:26
- Forum: ✎✎ Lycée
- Sujet: Démonstration dans Z svp
- Réponses: 5
- Vues: 536
Re: petite question svp
Bonjour,
Cela reviendrait peut-être a montrer que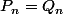 ? où
? où 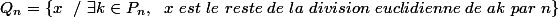
Cela reviendrait peut-être a montrer que
- 27 Fév 2019, 09:02
- Forum: ✎✎ Lycée
- Sujet: petite question svp
- Réponses: 6
- Vues: 841
Re: Relation d'ordre sur C
Bonsoir, Soit \leq une relation d'ordre définie par : \forall z \in \C : z \geq 0 \forall (z,z') \in \C^{*} , z \leq z' \Leftrightarrow ( |z|<|z'| )ou ( |z|=|z'| et Arg(z) \leq Arg(z') ) Je comprends pas le raisonnement suivant : 2 \leq 0 est faux car tou...
- 16 Juil 2018, 05:00
- Forum: ✯✎ Supérieur
- Sujet: Relation d'ordre sur C
- Réponses: 15
- Vues: 911
Re: Une équation différentielle
Dacu a écrit:Bonjour à tous,
Résoudre l'équation différentielle.
Cordialement,
Dacu
Dans IR ?
tu sais bien que la somme de deux réels superieurs ou égal à 0 est superieur ou égale à 0, donc
- 11 Mai 2018, 16:39
- Forum: ⚔ Défis et énigmes
- Sujet: Une équation différentielle
- Réponses: 3
- Vues: 751
Re: Exercice étude de fonction
Salut,
Alors tu ferais comment?
Alors tu ferais comment?
- 09 Mai 2018, 00:47
- Forum: ✎✎ Lycée
- Sujet: Exercice étude de fonction
- Réponses: 2
- Vues: 606
- 06 Mai 2018, 20:09
- Forum: ✯✎ Supérieur
- Sujet: Continuité fonction de plusieurs variables
- Réponses: 3
- Vues: 755
Re: Continuité fonction de plusieurs variables
Salut, et desole d'avance je n'ai pas d'accent sur mon qwerty, La projection est continue (car lineaire en dim finie) donc y -> y_1 et y ->y2 sont continues Faut peut-etre que tu montres que x -> (f(x), g(x)) est continue quand f et g sont continues (normalement c'est dans ton cours) le reste en dec...
- 03 Mai 2018, 18:39
- Forum: ✯✎ Supérieur
- Sujet: Continuité fonction de plusieurs variables
- Réponses: 3
- Vues: 755
Re: Forme quadratique et borne supérieure
J'ai un petit doute, le corrigé prend \theta < \tau Si \tau = Sup_{ \theta \in [0,1]} \{ \theta : r(\phi_{Q_{\theta}})=1\} est un ensemble qui contient qu'un élément qui est la borne supérieure du coup prendre un \theta strictement plus petit que la borne supérieure serait un non sens non ?...
- 02 Mai 2018, 05:56
- Forum: ✯✎ Supérieur
- Sujet: Forme quadratique et borne supérieure
- Réponses: 17
- Vues: 1213
Re: Forme quadratique et borne supérieure
Salut Infernaleur :) Merci bien pour ces précisions c'est plus clair. J'ai réussi à montrer que \theta' - \theta < a Par contre, je me demande pourquoi on pourrait pas prendre : \theta' = \theta + \frac{a}{2} au lieu de \theta' = Min (\theta + \frac{a}{2} , \tau + \frac{1-\tau}{2}&#...
- 01 Mai 2018, 06:51
- Forum: ✯✎ Supérieur
- Sujet: Forme quadratique et borne supérieure
- Réponses: 17
- Vues: 1213
Re: Forme quadratique et borne supérieure
Pour le cas où : \theta' = \frac{1+ \tau}{2} Dans ce cas \theta' = min(\theta +a/2, (\tau+1)/2) \leq \theta +a/2 car le min(x,y) <= x et <= y Donc \theta' - \theta \leq +a/2 < a Pour l'autre question: \theta \leq \tau , et ça va rien changer au raisonnement et les inégal...
- 01 Mai 2018, 06:42
- Forum: ✯✎ Supérieur
- Sujet: Forme quadratique et borne supérieure
- Réponses: 17
- Vues: 1213
Re: Forme quadratique et borne supérieure
nt qu'on a : x \in ] \tau-\epsilon , \tau [ Quelle est la méthode pour trouver le epsilon ? J'ai aussi | \theta - \theta'| < a \Rightarrow r(\phi_{Q_{\theta}})=r(\phi_{Q_{\theta'}}) \forall \epsilon > 0, \exists x dans E = \{ \theta \in [ 0,1] : r(\phi_{Q_{\theta}})\...
- 27 Avr 2018, 16:22
- Forum: ✯✎ Supérieur
- Sujet: Forme quadratique et borne supérieure
- Réponses: 17
- Vues: 1213
Re: Forme quadratique et borne supérieure
On est ainsi assuré que \tau < \theta ' < 1 et \theta' - \theta < a Pas compris pourquoi... . Franchement ca découle directement de ce que je viens de montrer en haut et de l'encadrement proposé. ( tu peux faire une distinction des cas si theta_prime = thera + a /2 puis si theta_prime = (1-...
- 27 Avr 2018, 05:51
- Forum: ✯✎ Supérieur
- Sujet: Forme quadratique et borne supérieure
- Réponses: 17
- Vues: 1213
Re: Forme quadratique et borne supérieure
Salut, Petit coup de pouce pour la premiere question, ca va peut-être te débloquer pour la suite. La définition de la borne sup: \forall \epsilon > 0, \exists x dans E = \{ \theta \in [ 0,1] : r(\phi_{Q_{\theta}})\} ) tq \tau - \epsilon < x , et \forall y \in E y < \tau bien sur On a donc x ...
- 27 Avr 2018, 05:42
- Forum: ✯✎ Supérieur
- Sujet: Forme quadratique et borne supérieure
- Réponses: 17
- Vues: 1213
Re: projection orthogonale
Bonjour, je n'arrive pas à résoudre ce problème : Le segment AB représente une grue dont la longueur mesure 18 mètres .Cette grue est fixée au sol au point A(12,12,0) et fait un angle de 50 degré avec le plan xy. Le segment AC représente sa projection orthogonale dans le plan xy et fait un angle de...
- 23 Avr 2018, 04:15
- Forum: ✎ Collège et Primaire
- Sujet: projection orthogonale
- Réponses: 1
- Vues: 662
Re: Matrices
2) b) Montrer que pour tout n \geq 1 on a D^nT=(-0,5)^nT. Je fais le produit matriciel à la main ou je fais une récurrence ? La recurrence semble à portée de main. Sinon un raisonnement direct marcherait aussi, vu que diag(a_1,a_2...,a_m)^n = diag(a_1^n,a_2^n..,a_m^n) , diag...
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
