Arithmétique

[Xavier]

Bonjour, j'aurais besoin d'aide pour résoudre cet exercice d'arithmétique ;

ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ
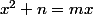
ㅤㅤㅤㅤㅤㅤㅤSoient et deux nombres premiers positifs tel que l'équation du second degré admet deux solutions entiers distincts. Déterminer les couples .

[raito123]

Bonjour,

Tu peux me rappeler comment tu résous une equation de second degrés en general stp? Ca sera ton point de départ.

[mathelot]

bonjour,
si x est une solution entière de l'équation, cherche à démontrer des relations comme
n|x ou x|n

[aymanemaysae]

Bonjour;

;

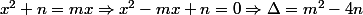
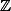
pour que cette équation ait deux solutions distinctes dans , il faut avoir

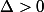
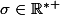
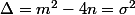
; donc il existe tel que ; donc : ;

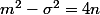
donc : .

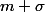
On remarque que et sont de même parité , donc paires .

De plus on a : .

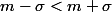
La conclusion est maintenant tout à fait directe .

[mathelot]

bonjour,
m et n sont premiers.

si et sont des solutions entières de


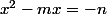
alors et divisent n,

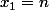
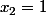
alors et car n est premier
d'où

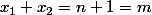
donc
n et n+1 sont des entiers premiers
donc n=2 et m=3

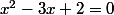
réciproquement, a deux racines entières distinctes.

[chan79]

salut
on peut remarquer que
n=mx-x²
n=x(m-x)
x divise n
comme n est premier, on a x=1 ou x=n

1°) cherchons les (m,n) de sorte que 1 soit une solution non unique
x²-mx+n=0
l'autre solution est x=n
m=n+1
seule possibilité
x²-3x+2=0 soit(m;n)=(2;3)

2°)cherchons les (m,n) telles que n soit une solution non unique
l'autre est 1
n²-mn+n=0
n=m+1
on retrouve (m,n)=(2;3)