2350 résultats trouvés
Revenir à la recherche avancée
Bonjour Antoine, étonnamment, il est assez pratique ici de prendre le cosinus. Car \cos\frac{\pi}{2}=0 ... Bien sûr, il ne suffit pas que les cosinus soient égaux pour que les angles soient égaux. Mais c'est une condition nécessaire. Le départ est donc : si x est une solution de l'équation, alors \a...
- 25 Oct 2015, 18:58
- Forum: ✯✎ Supérieur
- Sujet: Arcsin(x) + Arcsin(x*racinede(15))=pi/2
- Réponses: 8
- Vues: 1865
- 25 Aoû 2015, 15:19
- Forum: ✯✎ Supérieur
- Sujet: Probabilités et vecteurs : observation bizarre
- Réponses: 14
- Vues: 1073
stocke a écrit:Oui, je comprend maintenant bien pourquoi on obtient ces résultats. Par contre as-tu une idée de comment s'y prendre pour mettre ça en forme mathématiquement et déterminer la moyenne de la norme finale ?
Aucune idée !
- 25 Aoû 2015, 15:16
- Forum: ✯✎ Supérieur
- Sujet: Probabilités et vecteurs : observation bizarre
- Réponses: 14
- Vues: 1073
je ne pense pas qu'il soit difficile d'obtenir une norme qui vaut 1. D'ailleurs dans l'histogramme on voit que 1 tombe beaucoup plus souvent que 0.2 ou 1.7 par exemple. C'est juste qu'il tombe effectivement moins souvent que 0.9 et 1.1 par exemple. Oui, on est d'accord. C'était difficile relativeme...
- 25 Aoû 2015, 15:09
- Forum: ✯✎ Supérieur
- Sujet: Probabilités et vecteurs : observation bizarre
- Réponses: 14
- Vues: 1073
- 25 Aoû 2015, 15:06
- Forum: ✯✎ Supérieur
- Sujet: Probabilités et vecteurs : observation bizarre
- Réponses: 14
- Vues: 1073
Comme dit Beagle, les deux premiers vecteurs aident à bien comprendre le phénomène. Refais tes simulations avec juste 2 vecteurs (un de norme 1, et l'autre de norme 1/2) au lieu de 100. Tu verras déjà apparaître le phénomène : pas mal de normes accumulées autour de 1/2, encore plus autour de 3/2 (le...
- 25 Aoû 2015, 14:56
- Forum: ✯✎ Supérieur
- Sujet: Probabilités et vecteurs : observation bizarre
- Réponses: 14
- Vues: 1073
Bonjour, j'ai fait des simulations et j'obtiens aussi deux bosses dans l'histogramme. Une petite un peu en dessous de 1 et une grosse un peu au-dessus. Si tu regardes bien, le creux entre les deux bosses est exactement situé autour de la norme 1. Et j'ai l'intuition qu'il est effectivement difficile...
- 25 Aoû 2015, 14:40
- Forum: ✯✎ Supérieur
- Sujet: Probabilités et vecteurs : observation bizarre
- Réponses: 14
- Vues: 1073
Mais chaque chose en son temps. Il m'apparaissait plus urgent de commencer par remettre les choses solidement en place avant de considérer les cas particuliers peu intéressants. Se tromper dans la négation de "R est réflexive" méritait qu'on s'y attarde. C'est plus important à mon avis, qu...
- 23 Aoû 2015, 14:21
- Forum: ✯✎ Supérieur
- Sujet: relation dans un ensemble
- Réponses: 10
- Vues: 610
Robot a écrit:Ce n'est pas pareil si A a moins de 3 éléments. :lol3:
Merci, j'en ai bien conscience... Mais ce n'est pas la peine de troubler le message, du moins dans un premier temps.
- 23 Aoû 2015, 14:09
- Forum: ✯✎ Supérieur
- Sujet: relation dans un ensemble
- Réponses: 10
- Vues: 610
Bonjour Soit une relation R dans un ensemble À. R est symétrique pour toute paire d éléments, non réflexive (ne bouclé sur aucun élément) et, quels que soient à,b et c , trois éléments distincts de A, on vérifie aRb et bRc et aRc. Pour autant, quels que soient à et b éléments distincts de A (R est ...
- 23 Aoû 2015, 13:41
- Forum: ✯✎ Supérieur
- Sujet: relation dans un ensemble
- Réponses: 10
- Vues: 610
Je te conseille de séparer le cas où n est pair (tu peux écrire n=2p) et n est impair (n=2p+1) pour la démonstration.
- 21 Aoû 2015, 18:14
- Forum: ✯✎ Supérieur
- Sujet: Petit calcul
- Réponses: 4
- Vues: 462
- 21 Aoû 2015, 17:40
- Forum: ✯✎ Supérieur
- Sujet: Petit calcul
- Réponses: 4
- Vues: 462
- 26 Fév 2015, 12:43
- Forum: ✯✎ Supérieur
- Sujet: Serie numerique - calcul de somme
- Réponses: 13
- Vues: 1152
- 26 Fév 2015, 11:54
- Forum: ✯✎ Supérieur
- Sujet: Serie numerique - calcul de somme
- Réponses: 13
- Vues: 1152
Bonjour, Si une implication est vraie, sa contraposée est TOUJOURS vraie. Tu confonds peut-être avec la réciproque qui peut être vraie ou pas, selon les cas. Dans ton cas particulier, cela fonctionne évidemment. Le chemin logique est le suivant : si 0 n'est pas valeur propre, Ker(A-0In)={0} donc l'e...
- 26 Fév 2015, 11:40
- Forum: ✯✎ Supérieur
- Sujet: Question sur les valeurs propres
- Réponses: 2
- Vues: 501
As-tu prouvé que:
- T est une lci sur R\{1} ;
- si a,b sont dans R\{1}, alors aTb est dans R\{1};
- si a est dans R\{1}, alors son symétrique est encore dans R\{1}?
- 25 Fév 2015, 08:14
- Forum: ✯✎ Supérieur
- Sujet: Groupes
- Réponses: 11
- Vues: 713
Tu avais regardé un peu vite quand tu as trouvé que l'exercice était simple...
Non,) n'est pas un groupe !
n'est pas un groupe !
Non,
- 24 Fév 2015, 23:09
- Forum: ✯✎ Supérieur
- Sujet: Groupes
- Réponses: 11
- Vues: 713
Ncdk a écrit:Merci pour l'exercice, j'ai pu voir un peu, c'est un exercice plus facile que mes TD :p
Et alors,
- 24 Fév 2015, 19:36
- Forum: ✯✎ Supérieur
- Sujet: Groupes
- Réponses: 11
- Vues: 713
Bonsoir,
même dans le cadre actuel du programme de lÉducation Nationale, la limite de f en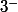 est bien -1. C'est par définition la limite de la restriction de f à
est bien -1. C'est par définition la limite de la restriction de f à 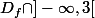 (crochet ouvert en 3), et on retrouve donc la notion de limite épointée...
(crochet ouvert en 3), et on retrouve donc la notion de limite épointée...
même dans le cadre actuel du programme de lÉducation Nationale, la limite de f en
- 24 Fév 2015, 19:07
- Forum: ✯✎ Supérieur
- Sujet: limites
- Réponses: 5
- Vues: 476
Oui c'est ça. Donc pour prouver que * est une lci sur G, il faut prendre deux éléments a et b, arbitrairement choisis dans G, et prouver que a*b est encore dans G. Plutôt que de deviser dans le vide, tu peux t'exercer sur l'exercice suivant : On définit sur R la loi ;) par a;)b = a + b ;) ab. 1. ( \...
- 24 Fév 2015, 19:00
- Forum: ✯✎ Supérieur
- Sujet: Groupes
- Réponses: 11
- Vues: 713
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
