335 résultats trouvés
Revenir à la recherche avancée
- 24 Avr 2021, 19:19
- Forum: ϟ Informatique
- Sujet: Python resultat d'arrangements.
- Réponses: 1
- Vues: 807
Re: Calcul de limite en - l'infini
Salut,
Si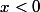 , alors
, alors 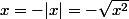 .
.
Si
- 10 Juil 2020, 12:33
- Forum: ✎✎ Lycée
- Sujet: Calcul de limite en - l'infini
- Réponses: 6
- Vues: 878
Re: Courbe paramétrée g(f) avec g(x) = f'(x)
Bonjour,
N'hésite pas à préciser ta demande au cas où tu as du mal à saisir nos réponses respectives.
Bon début de semaine !
N'hésite pas à préciser ta demande au cas où tu as du mal à saisir nos réponses respectives.
Bon début de semaine !
- 06 Juil 2020, 07:24
- Forum: ✯✎ Supérieur
- Sujet: Courbe paramétrée g(f) avec g(x) = f'(x)
- Réponses: 4
- Vues: 806
Re: Courbe paramétrée g(f) avec g(x) = f'(x)
Salut, J'ai du mal à comprendre la question. Si g est définit comme l'opérateur qui prend une fonction et t'en sort une autre beh c'est bon : g(f) est la fonction définie par x\mapsto f'(x) . Par contre si tu cherches g(f(x)) (où ici c'est g est une fonction qui t...
- 05 Juil 2020, 04:02
- Forum: ✯✎ Supérieur
- Sujet: Courbe paramétrée g(f) avec g(x) = f'(x)
- Réponses: 4
- Vues: 806
Re: La situation est grave !!
J'ai fait une purge... Merci, ça en devenait insoutenable. Les modérateurs ont réagi vite, mais - il me semble - ont eu quelques difficultés à faire dégager le gus (qui a eu le temps de spam presque 3000 messages pendant plusieurs jours quand même ...). Il faudrait peut-être penser à donner la poss...
- 05 Juil 2020, 03:56
- Forum: ⚑ À propos de ce site
- Sujet: La situation est grave !!
- Réponses: 10
- Vues: 1909
La situation est grave !!
Salut !
Comme vous pouvez le voir, le forum est complètement infesté de ces messages malveillants. Presque 1000 messages en moins d'une journée !!
Un admin/modo doit absolument régler la situation !! Quelqu'un connait le contact d'un admin/modo ?
Comme vous pouvez le voir, le forum est complètement infesté de ces messages malveillants. Presque 1000 messages en moins d'une journée !!
Un admin/modo doit absolument régler la situation !! Quelqu'un connait le contact d'un admin/modo ?
- 28 Juin 2020, 13:05
- Forum: ⚑ À propos de ce site
- Sujet: La situation est grave !!
- Réponses: 10
- Vues: 1909
Re: livres vacance d'été
[...] Pour les deux bouquin j’ai un problème je déteste l’anglais quand je suis obligé je fait l’effort mais là je pense que ce que cherche peu se trouver en français ou traduis du moins Si tu te destines à une carrière dans la recherche, je pense que c'est une excellente idée d'accroître ton angla...
- 01 Juin 2020, 22:42
- Forum: ⚜ Salon Mathématique
- Sujet: livres vacance d'été
- Réponses: 6
- Vues: 986
Re: Borne supérieure sur système linéaire de Vandermonde
Axeldinh a écrit:Bonjour,
[...]
ps : je ne sais pas d'où viennent ces <br/>... une astuce pour s'en débarasser ?
[...]
Salut,
Utilise \cr plutôt que \\.
- 01 Juin 2020, 18:39
- Forum: ✯✎ Supérieur
- Sujet: Borne supérieure sur système linéaire de Vandermonde
- Réponses: 10
- Vues: 708
Re: livres vacance d'été
La majorité des gros bouquins de physique mathématique sont anglophones et sont littéralement des bibles qui récapitulent tous les thèmes avec un formalisme certes plus rigoureux que de simples bouquins de physique mais moins rigoureux que des bouquins de maths pures. Les références célèbres (y en a...
- 01 Juin 2020, 16:55
- Forum: ⚜ Salon Mathématique
- Sujet: livres vacance d'été
- Réponses: 6
- Vues: 986
Re: Décomposition d'un vecteur dans une base
Bonjour,
Très généralement, il s'agit d'un simple changement de base. Tu n'en as jamais fait ? Tu as déjà la matrice de passage; les nouvelles coordonnées sont donc immédiates.
Très généralement, il s'agit d'un simple changement de base. Tu n'en as jamais fait ? Tu as déjà la matrice de passage; les nouvelles coordonnées sont donc immédiates.
- 09 Mai 2020, 14:18
- Forum: ✯✎ Supérieur
- Sujet: Décomposition d'un vecteur dans une base
- Réponses: 5
- Vues: 586
Re: Intersection de deux surfaces et gradient
Effectivement, d'après ce que j'ai lu sur l'autre topic; ça ne ressemble pas vraiment au topic que j'ai créé ici 2 ans de cela; d'autant plus que j'ai du mal à saisir sa question.
- 04 Mai 2020, 14:54
- Forum: ✯✎ Supérieur
- Sujet: Intersection de deux surfaces et gradient
- Réponses: 10
- Vues: 1276
Re: Intersection de deux surfaces et gradient
Salut,
Que ne comprends-tu pas dans ma démarche ?
Que ne comprends-tu pas dans ma démarche ?
- 04 Mai 2020, 12:14
- Forum: ✯✎ Supérieur
- Sujet: Intersection de deux surfaces et gradient
- Réponses: 10
- Vues: 1276
Re: Le plus petit entier n tel que
Salut,
Connais-tu la fonction logarithme népérien ?
Connais-tu la fonction logarithme népérien ?
- 10 Avr 2020, 03:50
- Forum: ✎✎ Lycée
- Sujet: Le plus petit entier n tel que
- Réponses: 4
- Vues: 690
Re: Intégration (Residus)
Oui c'est pas mal ça, oublie pas de faire le produit des 4 par contre (:
C'est normal, calculer des résidus de pôles d'ordre >1, c'est toujours frustrant ahah
C'est normal, calculer des résidus de pôles d'ordre >1, c'est toujours frustrant ahah
- 28 Mar 2020, 09:12
- Forum: ✯✎ Supérieur
- Sujet: Intégration (Residus)
- Réponses: 7
- Vues: 848
Re: Intégration (Residus)
Je note z_i un des pôles qui nous intéresse. En posant \gamma_{ij} = z_i - z_j , ainsi que z = z_i + h avec h \to 0 , nous avons ( i\neq j\neq k\neq \ell les indices des pôles): \large \dfrac{z^6}{(z^4+a^4)^2} = \dfrac{(z_i+h)^6}{\left(h(\gamma_{ij}+h)(\gamma_{ik}+h&#...
- 28 Mar 2020, 08:19
- Forum: ✯✎ Supérieur
- Sujet: Intégration (Residus)
- Réponses: 7
- Vues: 848
Re: Intégration (Residus)
C'est un peu chiant je présume d'évaluer ces dérivés, si tu veux y aller à coup de D.L; tu peux toujours poser z = z_j +h où z_j est un des pôles qui nous intéresse et les D.L se font franchement bien, moi perso les formules des résidus pour les pôles d'ordre n > 1 je ne les utilise jamais car elles...
- 28 Mar 2020, 07:24
- Forum: ✯✎ Supérieur
- Sujet: Intégration (Residus)
- Réponses: 7
- Vues: 848
Re: Le sujet de bac S de Pondichéry en 2012
Salut, Il semble évident que c'est du n'importe quoi mais je pense qu'ils ont bien vu au départ, car ils mentionnent bien que le champ est vertical. À mon avis ils se sont rendus compte trop tard qu'ils s'étaient trompés pour la force mais le sujet semblait bien formé pour vérifier si les étudiants ...
- 28 Mar 2020, 07:08
- Forum: ⚛ Physique
- Sujet: Le sujet de bac S de Pondichéry en 2012
- Réponses: 4
- Vues: 842
Re: Intégration (Residus)
Salut, Utilises le lemme de Jordan avec un demi-cercle de rayon infini. Pour les calculs de résidus, étant donné que ce ne sont pas des pôles simples; il y a une formule qui donne le résidu pour un pôle d'ordre n avec des dérivées successives mais je ne pense qu'elle soit prouvée par tous les profs,...
- 28 Mar 2020, 07:00
- Forum: ✯✎ Supérieur
- Sujet: Intégration (Residus)
- Réponses: 7
- Vues: 848
Re: interraction fondamentale et notion de champ
Il semble évident qu'on parle pas de mécanique quantique et "fonction d'onde" quand on enseigne les forces coulombiennes et la structure atomique aux lycéens ^^ Moi non plus je n'ai pas parlé de " fonction d'onde ". Je déteste dire des bêtises et je préfère laisser cela à ceux q...
- 27 Mar 2020, 19:06
- Forum: ⚛ Physique
- Sujet: interraction fondamentale et notion de champ
- Réponses: 12
- Vues: 1010
Re: interraction fondamentale et notion de champ
Distance proton-électron dans l’atome d’hydrogène Pure fiction. Regarder quand même les solutions de l'équation de Schrödinger. La différence entre " électron " et " onde électronique " est la même qu'entre chou vert et vert chou . Il semble évident qu'on parle pas de mécanique ...
- 27 Mar 2020, 17:44
- Forum: ⚛ Physique
- Sujet: interraction fondamentale et notion de champ
- Réponses: 12
- Vues: 1010
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
