Complexes

[Reynolds]

Bonjour, j'ai un problème sur un exo:

Trouver le module et argument de

a) 1+i(1+ )

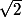
j'ai le module mais pas l'argument

b) +i(1- )

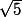
c)

J'ai le module du B mais je n'arrive pas a trouver les arguments et pour le dernier je ne vois pas mais j'ai penser a la formule de arg(z/z')

Merci d'avance

[Ericovitchi]

tu peux toujours dire pour un complexe a+ib que l'argument est arctan (b/a)

[Black Jack]

tu peux toujours dire pour un complexe a+ib que l'argument est arctan (b/a)

Pas si a < 0

exemple :
z = -1 + i

arctg(b/a) = arctg(-1) = - Pi/4
Mais -Pi/4 n'est par un argument de z = -1 + i

Si a < 0, alors arg(z) = Pi + arctg(b/a) (mod 2Pi)

:zen:

[Reynolds]

Ok merci beaucoup, mais j'ai pas vu cette formule en cours donc comment pourrais je faire autrement?

[Black Jack]

Ok merci beaucoup, mais j'ai pas vu cette formule en cours donc comment pourrais je faire autrement?

a)
|1 + i(1+V2)| = V(1² + (1+V2)²) = V(1 + 1 + 2 + 2V2) = V(4 + 2V2)

1 + i(1+V2) = V(4 + 2V2).(1/V(4 + 2V2) + i.(1+V2)/V(4 + 2V2))

cos(Phi) = 1/V(4 + 2V2)

sin(Phi) = (1+V2)/V(4 + 2V2)

--> Phi = (3Pi/8)

:zen:

[Reynolds]

Ah d'accord, c'est un angle remarquable je suis censé en apprendre d'autres?

Merci beaucoup.

[mathelot]

Ah d'accord, c'est un angle remarquable je suis censé en apprendre d'autres?

Merci beaucoup.

bonsoir



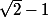
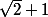
et sont inverses

[mathelot]

b) pour (b) , je ne savais pas comment faire

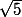
j'ai vû du alors j'ai élevé z à la puissance 5
avec la TI

je te donne les coeff du binome pour n=5 à tout hasard:
1 5 10 10 5 1

ça marche !! le résultat est fort simple. z est une racine cinquième

c) se traite différemment, c'est du calcul littéral et trigo

pour le (c)

- réduire au même dénominateur haut et bas
- factoriser par -i en haut et i en bas
- faire apparaitre

[mathelot]

c)

Bj,

on réduit au même dénominateur

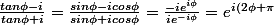[mathelot]

re,

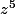
pour la (b) vaut 1024i.
Le souci, c'est d'avoir trouvé ça à la calculatrice.

je vois pas trop comment débuter, la partie réelle de z est une racine carrée (???). Ou alors , élever z au carré, tout simplement, et l'on tombe sur les lignes trigonométriques de l'angle polaire de mesure

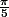
[Black Jack]

b)
|z|² = 10+2V5 + (1-V5)² = 10 + 2V5 + 1 + 5 - 2V5 = 16
|z| = 4

cos(Phi) = V(10+2V5)/4
sin(Phi) = (1-V5)/4
--> angle du 4ème quadrant.

Phi = -Pi/10
Mais ce n'est pas à retenir "par coeur".

:zen:

[Black Jack]

c)

arg(tan(PHI) - i)

a) si tan(PHI) > 0 :


phi1 = arctan(-1/tan(PHI)) (phi1 pour argument)

phi1 = arctan(-cotan(PHI))

phi1 = arctan(-tan((Pi/2)-PHI))

phi1 = -arctan(tan((Pi/2)-PHI))

phi1 = -Pi/2 + PHI
***
arg(tan(PHI) + i)

a) si tan(PHI) > 0

phi2 = arctan(1/tan(PHI))
...
phi2 = Pi/2 - Phi
***
Si tan(PHI) > 0 :

arg((tan(PHI)-i)/(tan(PHI+i)) = phi1 - phi2 = 2PHI - Pi
******
On recommence avec a) si tan(PHI) < 0 :

...

Et sauf erreur, on trouve pareillement : arg((tan(PHI)-i)/(tan(PHI+i)) = 2PHI - Pi

Essaie.

:zen: