équations inéquations
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
link2539
- Membre Naturel
- Messages: 11
- Enregistré le: 23 Mai 2009, 13:05
-
 par link2539 » 23 Mai 2009, 13:08
par link2539 » 23 Mai 2009, 13:08
bonjour a tous, voilà j'ai un problème je n'arrive pas à résoudre ces deux équations pouvez vous m'aider ???
(2x-5)^4 = 16
et
(2x-5)^4 <=16
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 23 Mai 2009, 13:10
par Timothé Lefebvre » 23 Mai 2009, 13:10
Bonjour,
passe tout du même côté, tu as une belle I.R ...
-
link2539
- Membre Naturel
- Messages: 11
- Enregistré le: 23 Mai 2009, 13:05
-
 par link2539 » 23 Mai 2009, 13:14
par link2539 » 23 Mai 2009, 13:14
le problème c'est que je n'arrive pas a développer (2x-5)^4 j'ai essayé tous se que je savais mais s'en résultat.
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 23 Mai 2009, 13:21
par Timothé Lefebvre » 23 Mai 2009, 13:21
Ne développe pas !
Tu vas avoir un PFN (produit de facteurs nul) ...
-
link2539
- Membre Naturel
- Messages: 11
- Enregistré le: 23 Mai 2009, 13:05
-
 par link2539 » 23 Mai 2009, 13:23
par link2539 » 23 Mai 2009, 13:23
donc je fais (2x-5)^4 - 16 = 0 ???
-
Cheche
- Membre Rationnel
- Messages: 650
- Enregistré le: 17 Avr 2009, 19:25
-
 par Cheche » 23 Mai 2009, 13:32
par Cheche » 23 Mai 2009, 13:32
Salut,
Oui et ici tu as une Identité Remarquable :
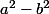
-
link2539
- Membre Naturel
- Messages: 11
- Enregistré le: 23 Mai 2009, 13:05
-
 par link2539 » 23 Mai 2009, 14:16
par link2539 » 23 Mai 2009, 14:16
donc si je suis vos conseille sa ferai (2x-5)^4 - 2^4 mais pour l'identité a2 - b2 je fais comment pour simplifier les puissance 4
-
link2539
- Membre Naturel
- Messages: 11
- Enregistré le: 23 Mai 2009, 13:05
-
 par link2539 » 23 Mai 2009, 14:18
par link2539 » 23 Mai 2009, 14:18
donc si je suis vos conseille sa ferai (2x-5)^4 - 2^4 = 0 mais pour l'identité a2 - b2 je fais comment pour simplifier les puissance 4
-
link2539
- Membre Naturel
- Messages: 11
- Enregistré le: 23 Mai 2009, 13:05
-
 par link2539 » 23 Mai 2009, 14:31
par link2539 » 23 Mai 2009, 14:31
oui mais il manque un (2x-5)^2
-
link2539
- Membre Naturel
- Messages: 11
- Enregistré le: 23 Mai 2009, 13:05
-
 par link2539 » 23 Mai 2009, 14:37
par link2539 » 23 Mai 2009, 14:37
alors si je suis ton conseille :((2x-5)^2 - (4)^2) ((2x-5)2 + (4)2)
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 23 Mai 2009, 14:38
par Timothé Lefebvre » 23 Mai 2009, 14:38
Oui, mais tu peux prendre les racines quadratiques et pas juste les carrées.
-
link2539
- Membre Naturel
- Messages: 11
- Enregistré le: 23 Mai 2009, 13:05
-
 par link2539 » 23 Mai 2009, 14:43
par link2539 » 23 Mai 2009, 14:43
donc après sa me donne :
 - (16^2 )) ((4x^2 - 25 ^2 ) + (16 ^2)))
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 23 Mai 2009, 14:48
par Timothé Lefebvre » 23 Mai 2009, 14:48
Pose d'abord
^4-2^4)
et on sait (ou on peut retrouver)
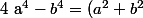(a^2-b^2))

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 23 Mai 2009, 14:54
par Ericovitchi » 23 Mai 2009, 14:54
Hum
Quand tu en es à
^2 - (4)^2) ((2x-5)^2 + (4)^2))
D'abord ne développes pas
^2 - (4)^2))
qui est un nouvel

Ensuites, ne te trompes pas dans le développement de
^2 + (4)^2))
^2=4x^2-20x+25)
-
link2539
- Membre Naturel
- Messages: 11
- Enregistré le: 23 Mai 2009, 13:05
-
 par link2539 » 23 Mai 2009, 14:57
par link2539 » 23 Mai 2009, 14:57
(2x-5)^4 - 2 ^4
= ((2x^2 - 5^2)+2^2) ((2x^2 - 5^2)-2^2)
=(4x^2-25^2+4^2) (4x^2-25^2-4^2)
et après je développe ?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 23 Mai 2009, 15:07
par Ericovitchi » 23 Mai 2009, 15:07
je me demande si tu ne fais pas l'erreur de croire que
^2 = a^2-b^2)
ce qui est complètement faux ?
^2=a^2+b^2-2ab)
-
link2539
- Membre Naturel
- Messages: 11
- Enregistré le: 23 Mai 2009, 13:05
-
 par link2539 » 23 Mai 2009, 15:07
par link2539 » 23 Mai 2009, 15:07
((4x^2-20x-25)-4^2) ((4x^2+20x+25)+4^2)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
