Complexes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ariimoana
- Messages: 7
- Enregistré le: 18 Oct 2008, 14:25
-
 par ariimoana » 18 Oct 2008, 14:28
par ariimoana » 18 Oct 2008, 14:28
Bonjour, une petite question car on me demande un module et un argument de z=1+sin(x)+icos(x),
j'arrive à un module au carré=2+2sin(x)
d'où le module : racine(2+2sin(x))=rac(2)*rac(1 +sin(x)) après on discute des conditions pour x là je n'y arrive pas trop pour x et puis il me reste l'arg par la suite.
Merci de bien vouloir m'aider
-
phryte
- Membre Irrationnel
- Messages: 1406
- Enregistré le: 05 Juil 2008, 17:09
-
 par phryte » 18 Oct 2008, 14:45
par phryte » 18 Oct 2008, 14:45
Slt.
soit z=a+ib alors
module de z: |z|=Racine_carré(a²+b²)
argument de z : cos(A)=a/|z| sin(A)=b/|z| ou tg(A)=b/a
...
-
triskaideka
- Membre Naturel
- Messages: 18
- Enregistré le: 08 Juil 2008, 09:19
-
 par triskaideka » 18 Oct 2008, 21:21
par triskaideka » 18 Oct 2008, 21:21
Pas besoin de discuter selon les valeurs de x , s'il est réel alors -1<=sin(x)<=1 donc t'as pas de problème dans ta racine. Mais j'ai peut être mas compris ton souci.

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 18 Oct 2008, 22:31
par fatal_error » 18 Oct 2008, 22:31
Salut,
On peut aussi remarquer que
=cos(\frac{\pi}{2}-x))
et
=sin(\frac{\pi}{2}-x))
soit
+isin(\frac{\pi}{2}-x))
et
}=e^{i(\frac{\frac{\pi}{2}-x}{2})}*2cos(\frac{\frac{\pi}{2}-x}{2})=e^{i(\frac{\pi}{4}-\frac{x}{2})}*2cos(\frac{\pi}{4}-\frac{x}{2}))
la vie est une fête

-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 18 Oct 2008, 22:37
par emdro » 18 Oct 2008, 22:37
Bonjour,
pense à l'angle moitié dans ce cas-là.
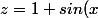+icos(x)=1+i(cosx-isinx)=1+ie^{-ix}=1+e^{i(\frac{\pi}{2}-x)}=e^{i(\frac{\pi}{4}-\frac{x}{2})}(e^{i(\frac{x}{2}-\frac{\pi}{4})}-e^{i(\frac{\pi}{4}-\frac{x}{2})}))
Avec une formule d'Euler, tu n'es pas loin du compte...
-
mathelot
 par mathelot » 19 Oct 2008, 06:26
par mathelot » 19 Oct 2008, 06:26
emdro a écrit:}=e^{i(\frac{\pi}{4}-\frac{x}{2})}(e^{i(\frac{x}{2}-\frac{\pi}{4})}) -
- }))
il y a une erreur de signe. il sort un cosinus.
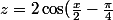 e^{i(\frac{\pi}{4}-\frac{x}{2})})
c'est la forme trigo de z ssi le cosinus est positif.
-
ariimoana
- Messages: 7
- Enregistré le: 18 Oct 2008, 14:25
-
 par ariimoana » 19 Oct 2008, 09:57
par ariimoana » 19 Oct 2008, 09:57
merci de m'avoir éclaircit :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
