Bonjour,
Mon intuition me dit que l'ensemble des 2^n/3^m (m et n dans N) est dense dans R+, mais je n'arrive pas à le démontrer.
Quelqu'un a-t-il une idée ?
Merci
Densité
11 messages
- Page 1 sur 1
Re: densité
C'est bien sûr la bonne idée , on peut aussi prendre m et n dans Z pour utiliser ensuite un résultat connu .
Imod
Imod
Re: densité
Je cherche n et m tels que a<(2^n/3^m)<b, pour a et b arbitraires.
Je passe aux logarithmes, et je dois construire n et m tels que :
ln(a)/mln(2) + ln(3)/ln(2) < m/n < ln(b)/mln(2) + ln(3)/ln(2).
Ce qui me semble faisable, mais je ne vois pas précisément comment.
Merci pour votre aide.
P. S. : quel est donc ce résultat "connu" ?
Je passe aux logarithmes, et je dois construire n et m tels que :
ln(a)/mln(2) + ln(3)/ln(2) < m/n < ln(b)/mln(2) + ln(3)/ln(2).
Ce qui me semble faisable, mais je ne vois pas précisément comment.
Merci pour votre aide.
P. S. : quel est donc ce résultat "connu" ?
Re: densité
Bonjour
Je pense que l'exercice 2 du lien suivant devrait t'éclairer
https://perso.eleves.ens-rennes.fr/peop ... de%20R.pdf
Je pense que l'exercice 2 du lien suivant devrait t'éclairer
https://perso.eleves.ens-rennes.fr/peop ... de%20R.pdf
Re: densité
Merci beaucoup !
Je n'ai pas encore regardé en détail, mais je pense qu'avec ça je vais y arriver.
Je vous tiens au courant.
Paquito.
Je n'ai pas encore regardé en détail, mais je pense qu'avec ça je vais y arriver.
Je vous tiens au courant.
Paquito.
Re: densité
J'ai repris ma recherche sur mon exercice. J'obtiens que l'ensemble des 2^n/3^m est dense dans R*+, pour n et m dans Z. Mais qu'en est-il pour n et m dans N ? Pour ce que je veux en faire, des fréquences musicales, via des divisions de cordes, j'ai besoin que n et m soient positifs.
Merci pour vos idées.
Paquito
Merci pour vos idées.
Paquito
Re: densité
Si  est un réel strictement positif . On cherche des entiers naturels
est un réel strictement positif . On cherche des entiers naturels  et
et  tels que
tels que  soit aussi proche que l’on veut de
soit aussi proche que l’on veut de  . En notant
. En notant 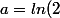 , b=ln(3)) et
et 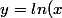) , on est ramené à chercher
, on est ramené à chercher  et
et  pour que
pour que  puisse approcher
puisse approcher  autant qu’on le souhaite . Comme les parties fractionnaires de
autant qu’on le souhaite . Comme les parties fractionnaires de  sont denses dans
sont denses dans  ,
,  peut approcher
peut approcher  à volonté . Il reste à multiplier par b pour conclure .
à volonté . Il reste à multiplier par b pour conclure .
Imod
Imod
Re: densité
Bonjour,
Merci pour ta réponse.
Mais d'une part, y/b pourrait ne pas appartenir à [0,1].
Et d'autre part, où est passé le m ?
Ou quelque chose m'échappe ?
Merci.
Paquito
Merci pour ta réponse.
Mais d'une part, y/b pourrait ne pas appartenir à [0,1].
Et d'autre part, où est passé le m ?
Ou quelque chose m'échappe ?
Merci.
Paquito
Re: densité
Bonjour
Je pense qu'imod a voulu dire que
 peut approcher la partie fractionnaire de
peut approcher la partie fractionnaire de  à volonté
à volonté
Donc
 approche
approche 
ou
 approche
approche 
et en multipliant par b :
 approche
approche 
On aurait donc m=
Mais là se pose la question de savoir si m est positif...
Je pense qu'imod a voulu dire que
Donc
ou
et en multipliant par b :
On aurait donc m=
Mais là se pose la question de savoir si m est positif...
Re: densité
Bonjour,
On passe au logarithme : l'exercice revient à montrer que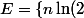-m\ln(3)\mid m,n \in \mathbb N\}) est dense dans
est dense dans  .
.
Le résultat classique sur les sous-groupes additifs de) entraîne que
entraîne que 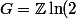+\mathbb Z \ln(3)) est dense dans
est dense dans  , puisque
, puisque /\ln(3)) est irrationnel.
est irrationnel.
Soit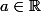 et cherchons à approcher
et cherchons à approcher  par un élément de
par un élément de  à moins de
à moins de 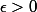 donné. D'après le résultat rappelé plus haut, il existe
donné. D'après le résultat rappelé plus haut, il existe  tel que
tel que )) . Le minimum avec
. Le minimum avec ) sert à s'assurer que
sert à s'assurer que  ou
ou  est dans
est dans  .
.
Supposons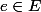 . et choisissons un entier naturel
. et choisissons un entier naturel  tel que
tel que \leq a) . Alors il existe un (unique) entier naturel
. Alors il existe un (unique) entier naturel  tel que
tel que +\ell e\leq a<-k\ln(3)+(\ell+1)e) . On a encadré
. On a encadré  entre deux éléments de
entre deux éléments de  distants de moins de
distants de moins de  , c'est gagné.
, c'est gagné.
Je te laisse gagner dans le cas .
.
On passe au logarithme : l'exercice revient à montrer que
Le résultat classique sur les sous-groupes additifs de
Soit
Supposons
Je te laisse gagner dans le cas
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
