Applications linéaire/polynômes

[Cubiste]

Bonjour,

On considère f une application linéaire de R[X] ----> R[X] qui a P(X)---->P(X+1) et on me demande de déterminer les images de la base canonique de R[X] par f puis d'en déduire les propriétés de f.
La base canonique de f c'est X^n mais du coup son image par f c'est (X+1)^n mais je sais pas quoi faire a partir de là...
Avez-vous une idée?

Merci

[tournesol]

F induit pour tout entier naturel k une bijection de sur lui même . A démontrer .
En déduire que f est bijective.
On peut déterminer les valeurs propres et les polynômes propres si tu as vu tout cela en cours

[pascal16]

FBN ?

[aviateur]

Bonjour
L'opérateur f (comme application linéaire de R[X] vers lui même) est évidemment bijectif et
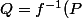est défini par Q(X)=P(X-1).
Ensuite que soit stable par f est évident. Concernant les valeurs propres éventuelles, soit
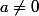une valeur propre de vecteurs propres P, on
P(X+1)=a P(X). En regardant dans chaque membre le terme de plus haut degré, on voit que nécessairement
a=1. Donc P(X)=P(X+1) et cela implique directement que P=c (c= constante.)
Pour le voir il y a plusieurs façons, comme par exemple si P n'est pas constant alors en se plongeant dans , P a au moins une racine il en est de même pour
ce qui n'est pas possible. En conclusion f admet une seule valeur propre et le sev propre est engendré par P=1.
Alors le problème c'est que dire de plus de f? Je ne vois pas trop.
Alors que faire avec la question?
Je pense alors qu'on peut fixer k, et on écrit la matrice de f restreint à dans la base
et éventuellement retrouver d'une autre façon les résultats ci dessus.

[tournesol]

Merci aviateur . Tes deux premières lignes d'explications nous rappellent qu'il ne faut pas oublier ses bases: f de E dans F et g de F dans E telles que gof=IdE et fog=Id F
Alors f et g sont bijectives et g=