A l'aide

[JMO]

svp jai pas pu résoudre cette qst
soit une suite réelle (Un) bornée telle que la suite (U(n+1) -Un) est monotone: montrer que(Un) est convergente

[JasonG]

Théorème de convergence monotone. En gros:
Toute suite croissante majorée est convergente.
Toute suite décroissante minorée est convergente.
Ta suite est monotone (donc croissante ou décroissante) et bornée (donc majorée et minorée)

Ce n'est peut etre pas super rigoureux, mais il me semble que c'est l'idée

[JMO]

mais on m'a rien dit a propos de Un je ne sais po s'il est monotone je sais juste qu'il est bornée

[Ben314]

Salut
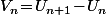
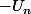
Si tu pose pour tout alors tu peut supposer croissante (quitte à changer en ) et, vu que cette suite , c'est surtout son signe qui t’intéresse (c'est lui qui donne la monotonie de , tu traite deux cas de figures :
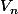
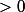
1) Soit l'un des est et alors . . .
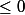
2) Soit tout les sont et . . .

[JMO]

mrc bien