Aide pour resoudre des problemes d'examen
60 messages
- Page 2 sur 3 - 1, 2, 3
just do it
je n'ai pas l'impression que tu te creuses vraiment la tête.
Tu es en train de faire faire tout ton devoir par d'autres et c'est pas une solution...
Tu es en train de faire faire tout ton devoir par d'autres et c'est pas une solution...
Salut,
normalement, pour les congruences, en traitant les "équations" de congruence 2 à 2, on obtient à chaque fois une équation diophantienne dont on trouve l'ensemble des solutions... Je pense qu'on doit pouvoir s'en tirer comme ça, en tout cas c'est une piste à exploiter, mais personnellement je n'ai pas essayé de le faire.
:happy3:
normalement, pour les congruences, en traitant les "équations" de congruence 2 à 2, on obtient à chaque fois une équation diophantienne dont on trouve l'ensemble des solutions... Je pense qu'on doit pouvoir s'en tirer comme ça, en tout cas c'est une piste à exploiter, mais personnellement je n'ai pas essayé de le faire.
:happy3:
Je remets le sujet ou j'ai besoin d'aide
Salut,
Galt ,je voudrais savoir si tu as réussi à faire la question 6.
Si,ce n'est pas le cas est-ce que quelqu'un sait comment si prendre.
Morpheus a écrit:Salut,
j'ai besoin d'aide sur ce probleme
Soit n un entier. On appelle composition de n toute suite finie () d'entiers strictements positifs dont la somme fait n.
Les entiers sont appelés parts de la composition , p est la longueur de la composition.
Par exemple (4, 2, 3), (3, 2, 4) et (4, 4, 1) sont trois compositions de 9 de longueurs 3. Soitle nombre de composition de n de longueur p. On se gardera de confondre
avec le coefficient binomial
.
1)Calculerpour n et p inférieur ou égal à 4.
2)Montrer que le nombre de compositions de n de longueur p et dont la première part est 1 est égal au nombre de compositions de n-1 de longueur p-1 .
3)Montrer que le nombre de compositions de n de longueur p et dont la première part est différente de 1 est égal au nombre de compositions de n-1 de longueur p.
4)Soit la série génératrice
Montrer que
5)En déduire que:
6)Montrer que le coefficient dedans f(z,t) est égale à
. Indication : Écrire f(z,t) sous la forme
Merci d'avance a ceux qui répondront
Galt a écrit:Bonjour
Pour les dénombrements :
Si la première part est 1, il reste p-1 nombres de somme n-1, ce qui est bien.
Si la première part est strictement supérieure à 1, en lui enlevant 1 j'obtiens une décomposition de n-1 en p parts, soit(la réciproque est évidente)
On a donc pour n > 1, la même relation de récurrence que les combinaisons.
En revanche,,
,
et
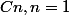
Essayons d'écrire une relation de récurrence
Compte tenu de, et en changeant les indices, j'obtiens
Soitet la formule proposée doit s'en déduire
Pour, on a une somme de série géométrique au facteur z près.
Pour la question 6, la forme proposée me semble bizarre.Je fais les calculs et j'arrive
Salut,
Galt ,je voudrais savoir si tu as réussi à faire la question 6.
Si,ce n'est pas le cas est-ce que quelqu'un sait comment si prendre.
Si tu as fait la question 5, tu t'es aperçu d'une erreur dans l'énoncé que tu as transcrit: dans le dénominateur de f(z,t) , t est en facteur et non en exposant de (1+z); en d'autre termes,
f(z,t)=zt/(1-(1+z)t)=(zt/(1-t))/(1-zt/(1-t)) soit x/(1-x) avec x=zt/(1-t)
Il n'y a plus qu'à developper la série entière x/(1-x) de terme général x^n
n de 1 à l'infini...
f(z,t)=zt/(1-(1+z)t)=(zt/(1-t))/(1-zt/(1-t)) soit x/(1-x) avec x=zt/(1-t)
Il n'y a plus qu'à developper la série entière x/(1-x) de terme général x^n
n de 1 à l'infini...
palmade a écrit:Si tu as fait la question 5, tu t'es aperçu d'une erreur dans l'énoncé que tu as transcrit: dans le dénominateur de f(z,t) , t est en facteur et non en exposant de (1+z); en d'autre termes,
f(z,t)=zt/(1-(1+z)t)=(zt/(1-t))/(1-zt/(1-t)) soit x/(1-x) avec x=zt/(1-t)
Il n'y a plus qu'à developper la série entière x/(1-x) de terme général x^n
n de 1 à l'infini...
Je ne comprends pas ce que tu dis.
Est-ce que ce que la question 4 est bonne,et comment faire le reste?
Ce que tu as écrit répond a quelle question?
Merci de me répondre
Il me semble que le message de Galt (#16) répondait à la question 4 (ou presque puisqu'il donne une relation de récurrence multiplicative)
Mon message précédent indique qu'alors la question 5, en sommant la série de terme général z(1+z)^(n-1)t^n on obtient zt/(1-(1+z)t)
Je donne ensuite la solution de la question 6 que tu réclamais à cors et à cris!
Mon message précédent indique qu'alors la question 5, en sommant la série de terme général z(1+z)^(n-1)t^n on obtient zt/(1-(1+z)t)
Je donne ensuite la solution de la question 6 que tu réclamais à cors et à cris!
Je remets le sujet ou j'ai besoin d'aide
Salut,
est ce que quelqu'un pourrait me détailler les calculs fait à partir de la question 4 car en essayant de les refaire,je n'arrive pas à trouver les résultats.
Merci d'avance
Morpheus a écrit:Salut,
j'ai besoin d'aide sur ce probleme
Soit n un entier. On appelle composition de n toute suite finie () d'entiers strictements positifs dont la somme fait n.
Les entiers sont appelés parts de la composition , p est la longueur de la composition.
Par exemple (4, 2, 3), (3, 2, 4) et (4, 4, 1) sont trois compositions de 9 de longueurs 3. Soitle nombre de composition de n de longueur p. On se gardera de confondre
avec le coefficient binomial
.
1)Calculerpour n et p inférieur ou égal à 4.
2)Montrer que le nombre de compositions de n de longueur p et dont la première part est 1 est égal au nombre de compositions de n-1 de longueur p-1 .
3)Montrer que le nombre de compositions de n de longueur p et dont la première part est différente de 1 est égal au nombre de compositions de n-1 de longueur p.
4)Soit la série génératrice
Montrer que
5)En déduire que:
6)Montrer que le coefficient dedans f(z,t) est égale à
. Indication : Écrire f(z,t) sous la forme
Merci d'avance a ceux qui répondront
Galt a écrit:Bonjour
Pour les dénombrements :
Si la première part est 1, il reste p-1 nombres de somme n-1, ce qui est bien.
Si la première part est strictement supérieure à 1, en lui enlevant 1 j'obtiens une décomposition de n-1 en p parts, soit(la réciproque est évidente)
On a donc pour n > 1, la même relation de récurrence que les combinaisons.
En revanche,,
,
et
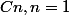
Essayons d'écrire une relation de récurrence
Compte tenu de, et en changeant les indices, j'obtiens
Soitet la formule proposée doit s'en déduire
Pour, on a une somme de série géométrique au facteur z près.
Pour la question 6, la forme proposée me semble bizarre.Je fais les calculs et j'arrive
Salut,
est ce que quelqu'un pourrait me détailler les calculs fait à partir de la question 4 car en essayant de les refaire,je n'arrive pas à trouver les résultats.
Merci d'avance
Je pensais être clair, mais je détaille...
Galt a abouti à fn=(1+z)f(n-1) et comme f1=z, fn=z(1+z)^(n-1): voilà pour la question 4!
question 5: la série de terme général fn*t^n=(zt)*(t(1+z))^(n-1) est au facteur zt près, une série géométrique y^(n-1) avec y=t(1+z), qui part de n-1=0; sa somme est donc zt*(1/(1-y))=zt/(1-t(1+z))
question 6:1-t(1+z)=1-t-zt=(1-t)(1-zt/(1-t)
donc f(z,t)=zt/(1-t(1+z))=(zt/(1-t))/(1-zt/(1-t)) soit x/(1-x) avec x=zt/(1-t)
qui est égal à la somme à partir de n=1 de la série x^n soit (zt/(1-t))^n
Le coefficient de z^n est donc (t/1-t))^n
cqfd
Galt a abouti à fn=(1+z)f(n-1) et comme f1=z, fn=z(1+z)^(n-1): voilà pour la question 4!
question 5: la série de terme général fn*t^n=(zt)*(t(1+z))^(n-1) est au facteur zt près, une série géométrique y^(n-1) avec y=t(1+z), qui part de n-1=0; sa somme est donc zt*(1/(1-y))=zt/(1-t(1+z))
question 6:1-t(1+z)=1-t-zt=(1-t)(1-zt/(1-t)
donc f(z,t)=zt/(1-t(1+z))=(zt/(1-t))/(1-zt/(1-t)) soit x/(1-x) avec x=zt/(1-t)
qui est égal à la somme à partir de n=1 de la série x^n soit (zt/(1-t))^n
Le coefficient de z^n est donc (t/1-t))^n
cqfd
palmade a écrit:Je pensais être clair, mais je détaille...
Galt a abouti àet comme
,
: voilà pour la question 4!
question 5: la série de terme généralest au facteur zt près, une série géométrique
avec
, qui part de n-1=0; sa somme est donc
=\frac{zt}{1-t(1+z)})
question 6:=1-t-zt=(1-t)\frac{1-zt}{1-t})
doncsoit
avec
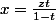
qui est égal àsoit
^n)
Le coefficient deest donc
^n)
cqfd
Merci Palmade pour ces détails et est-ce que j'ai bien mis ce que tu as écrit en écriture mathematiques?
OK pour la transcription sauf à la fin de la ligne question 6 où il manquait une parenthèse dans mon écriture; lire (1-t)(1-zt/(1-t)) donc le (1-t) ne divise que zt...
Je sais pas utiliser Tex avec le clavier de mon Powerbook qui est un peu différent des PC...
Pour sept-épées, je ne suis pas sur que Morpheus connaisse le lemme chinois, d'où mon approche plus pragmatique...(il y a une faute de frappe dans le cours de ma solution: lire modulo 2640 et non 240)
Je sais pas utiliser Tex avec le clavier de mon Powerbook qui est un peu différent des PC...
Pour sept-épées, je ne suis pas sur que Morpheus connaisse le lemme chinois, d'où mon approche plus pragmatique...(il y a une faute de frappe dans le cours de ma solution: lire modulo 2640 et non 240)
palmade a écrit:Les quatre congruences ont des modules premiers entre eux deux à deux
x-1 est divisible par 48 et x-2 par 55 donc 55(x-1)-48(x-2)=7x+41 est divisible par 55*48=2640. Reste à trouver un nombre congru à 41 modulo 2640, divisible par 7: 2640+41=2681=383*7 convient
Donc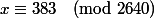
Salut,
je voudrais savoir si cette méthode marche lorsque les restes sont tous différents.
par exemple si on a
Si, cette méthode ne marche pas pour le cas que j'ai évoqué est-ce que tu pourrais m'indiquer comment on fait lorsqu'il faut prendre les congruences 2 à 2 avec l'énoncé qui était le suivant.
Trouver le plus petit entier x > 0 vérifiant simultanement les congruences
ps:Palmade ,je te mets un lien,si ça t'interesse, sur une page qui donne tous les symboles mathématiques en tex.Pour ecrire en tex,tu clique sur TEX et tu insere les symboles qu'il faut.
Voici le lien :http://fr.wikipedia.org/wiki/Aide:Formules_TeX
J'ai répondu à la question sur les restes chinois ici : http://maths-forum.com/showthread.php?p=23849#post23849 dans le cas de deux restes, on recommence pour les suivants.
Morpheus a écrit:Salut,
je poste un nouvel exercice:
Soit x un nombre. On définit par récurrence la suitepar
et
pour tout n > 0
1)Montrer par récurrence que;
Voici ce que j'ai fait:
On vérifie la récurrence pour n = 0et
donc OK
Supposons que la récurrence est vraie pour tout n>0 et démontrons qu'elle est vraie au rang suivant n+1
-(n+1)}{(n+1)})

 + n+1)
donc
2)En déduire la valeur de
Pour cette question, j'essaye de calculer
je fais
1) partie gauche du = et 2) partie droite.
1)
Le ? correspond à
2)
Pour X=1
Mais après je ne sais pas comment faire.
De plus ,je voudrais savoir si ma méthode est bonne car elle prend du temps.
En voici un autre
On appelle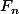 le n-ième nombre de Fibonacci :
le n-ième nombre de Fibonacci : 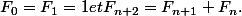
On rapelle que=\sum_{k=0}^\infty F_{k}z^k = {1 \over 1-z-z^2})
1)On définit la suite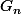 par
par
pout tout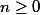
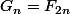
Établir une relation de récurence vérifiée par les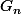
Ce que j'ai trouvé
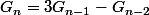 pour tout
pour tout 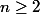
2)En deduire que=\sum_{k=0}^\infty G_{k}z^k={1-z \over 1-3z+z^2})
C'est fait
3)Retrouvez ce résultat en utilisant f(z).
C'est fait
4)Montrez que pour tout entier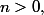 il existe une suite croissante finie
il existe une suite croissante finie 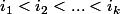 d'insices,telle que :
d'insices,telle que :
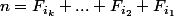
5)Montrez qu'il y a unicité de la suite si l'on impose
(a)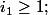
(b)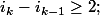
On appelle
On rapelle que
1)On définit la suite
pout tout
Établir une relation de récurence vérifiée par les
Ce que j'ai trouvé
2)En deduire que
C'est fait
3)Retrouvez ce résultat en utilisant f(z).
C'est fait
4)Montrez que pour tout entier
5)Montrez qu'il y a unicité de la suite si l'on impose
(a)
(b)
60 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
