je révise pour mes rattrapages de septembre et je voudrais savoir si quelqu'un pouvait m'indiquer comment répondre a cette question
Exercice 1
Soit
a)Calculer
b)Calculer la série génératrice
A(x) =
c)En déduire la valeur de
N_comme_Nul a écrit:Salut !
Pour la question (a), ...
Pour la (b), je n'avais jamais vu ça ... mais bon. Je me lance.
On a
On part de la relation de récurrence :
[INDENT][/INDENT]
On multiplie le tout par:
[INDENT][/INDENT]
En supposant que tout se passe bien, en sommant, on obtient :
[INDENT][/INDENT]
donc
[INDENT][/INDENT]
c'est-à-dire
[INDENT][/INDENT]
Je te laisse terminer pour en déduire.
Je ne sais pas si ça va t'aider, mais bon.
Surtout ... ne me tuez pas pour les conneries que j'ai pu dire.
Morpheus a écrit:Salut,
j'ai besoin d'aide sur ce probleme
Soit n un entier. On appelle composition de n toute suite finie () d'entiers strictements positifs dont la somme fait n.
Les entiers sont appelés parts de la composition , p est la longueur de la composition.
Par exemple (4, 2, 3), (3, 2, 4) et (4, 4, 1) sont trois compositions de 9 de longueurs 3. Soitle nombre de composition de n de longueur p. On se gardera de confondre
avec le coefficient binomial
.
1)Calculerpour n et p inférieur ou égal à 4.
2)Montrer que le nombre de compositions de n de longueur p et dont la première part est 1 est égal au nombre de compositions de n-1 de longueur p-1 .
3)Montrer que le nombre de compositions de n de longueur p et dont la première part est différente de 1 est égal au nombre de compositions de n-1 de longueur p.
4)Soit la série génératrice
Montrer que
5)En déduire que:
6)Montrer que le coefficient dedans f(z,t) est égale à
. Indication : Écrire f(z,t) sous la forme
Merci d'avance a ceux qui répondront
Galt a écrit:Bonjour
Pour les dénombrements :
Si la première part est 1, il reste p-1 nombres de somme n-1, ce qui est bien.
Si la première part est strictement supérieure à 1, en lui enlevant 1 j'obtiens une décomposition de n-1 en p parts, soit(la réciproque est évidente)
On a donc pour n > 1, la même relation de récurrence que les combinaisons.
En revanche,,
,
et
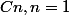
Essayons d'écrire une relation de récurrence
Compte tenu de, et en changeant les indices, j'obtiens
Soitet la formule proposée doit s'en déduire
Pour, on a une somme de série géométrique au facteur z près.
Pour la question 6, la forme proposée me semble bizarre.Je fais les calculs et j'arrive
Morpheus a écrit:Salut,
je poste un nouvel exercice:
Soit x un nombre. On définit par récurrence la suitepar
et
pour tout n > 0
1)Montrer par récurrence que;
Voici ce que j'ai fait:
On vérifie la récurrence pour n = 0et
donc OK
Supposons que la récurrence est vraie pour tout n>0 et démontrons qu'elle est vraie pour n+1
-(n+1)}{(n+1)})

 + n+1)
donc
2)En déduire la valeur de
(i)pour tout n > 0
(ii)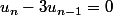
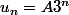
On cherche une solution particulière de la forme :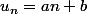
En remplaçant dans (i) on a: + b) = n)
ce qui donne
et aveccela donne

et donc
Morpheus a écrit:Salut,
j'ai besoin d'aide sur ce probleme
Soit n un entier. On appelle composition de n toute suite finie () d'entiers strictements positifs dont la somme fait n.
Les entiers sont appelés parts de la composition , p est la longueur de la composition.
Par exemple (4, 2, 3), (3, 2, 4) et (4, 4, 1) sont trois compositions de 9 de longueurs 3. Soitle nombre de composition de n de longueur p. On se gardera de confondre
avec le coefficient binomial
.
1)Calculerpour n et p inférieur ou égal à 4.
2)Montrer que le nombre de compositions de n de longueur p et dont la première part est 1 est égal au nombre de compositions de n-1 de longueur p-1 .
3)Montrer que le nombre de compositions de n de longueur p et dont la première part est différente de 1 est égal au nombre de compositions de n-1 de longueur p.
4)Soit la série génératrice
Montrer que
5)En déduire que:
6)Montrer que le coefficient dedans f(z,t) est égale à
. Indication : Écrire f(z,t) sous la forme
Merci d'avance a ceux qui répondront
Galt a écrit:Bonjour
Pour les dénombrements :
Si la première part est 1, il reste p-1 nombres de somme n-1, ce qui est bien.
Si la première part est strictement supérieure à 1, en lui enlevant 1 j'obtiens une décomposition de n-1 en p parts, soit(la réciproque est évidente)
On a donc pour n > 1, la même relation de récurrence que les combinaisons.
En revanche,,
,
et
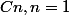
Essayons d'écrire une relation de récurrence
Compte tenu de, et en changeant les indices, j'obtiens
Soitet la formule proposée doit s'en déduire
Pour, on a une somme de série géométrique au facteur z près.
Pour la question 6, la forme proposée me semble bizarre.Je fais les calculs et j'arrive
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :