Matrice inversible

[Released]

bonjour
voici une question qui me bloque depuis quelques temps:

soit M une matrice carrée.
Montrer que s'il existe k un entier naturel non nul, tel que M^k = 0 , alors la matrice (I - M) est inversible.


j'ai un raisonnement bancal avec les déterminants:
M^k = 0 => det(M^k) = 0 => (det(M))^k = 0 => det(M) = 0
or det (M) = 0 équivaut à " une des lignes / colonnes est combinaison linéaire d'autres lignes / colonnes "

donc M a une colonne/ ligne combinaison linéaire des autres
or si on fait I - M c'est plus le cas => det(I-M) différent de 0 => I-M inversible

je suis presque sûr qu'il ne faut pas faire comme ça, mais même en y réfléchissant bien je n'aboutis à rien ^^'

en espérant que vous pourrez me donner un indice,
bonne soirée

[aviateur]

Bonjour
Soit k le plus petit entier tel que
Calcules alors et tu verras....

[Pseuda]

donc M a une colonne/ ligne combinaison linéaire des autres
or si on fait I - M c'est plus le cas => det(I-M) différent de 0 => I-M inversible

Bonjour,

Cela ne va pas, pourquoi ce n'est plus le cas ?

Une idée : si k=2, calcule (I-M)(I+M). Il suffit ensuite de généraliser.

Pas vu le message d'aviateur (k n'a pas besoin d'être le plus petit).

On peut traiter à part le cas k=1.

[aviateur]

Bonjour @pseuda
Pas vu ton message non plus.
Oui, mais ajouter des puissances nulles c'est pas très habituel. C'est pour moi une sorte de réflexe.

[Released]

Merci pour votre aide

[Carpate]

I-M inversible ssi ker(I-M) réduit au vecteur nul

Cherchons ker(I-M) :
C'est l'ensemble des vecteurs V non nuls tels que (I-M) V = 0 soit MV = V
V appartient au sous-espace vectoriel associé à la valeur propre 1
Or le polynôme minimal de M est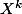 = 0 donc toutes les valeurs propres de M sont nulles
Donc ker(I-M) est réduit au vecteur nul et M est inversible