Valeurs propres et matrice non inversible
22 messages
- Page 1 sur 2 - 1, 2
Valeurs propres et matrice non inversible
Bonsoir,
Je souhaite comprendre le théorème qui dit que "Un nombre lambda est valeur propre de A(une matrice carrée) si et seulement si PA(lambda) =0". J'ai noté PA le polynôme caractéristique de A.
Voilà la démonstration que j'ai, avec en gras et soulignée la partie que je ne comprends pas (je ne fais pas le lien avec la première phrase juste avant). Hormis ça, je comprends, mais bon, c'est le coeur du truc :/
"Un nombre lambda est une valeur propre de A s'il existe un vecteur colonne X non nul tel que AX=lambda*X. Cela revient exactement à dire que la matrice A - lambda*In n'est pas inversible donc que det(A-lambda*In)=0 c'est-à-dire PA(lambda) =0"
Quel est le lien?
Merci!
Je souhaite comprendre le théorème qui dit que "Un nombre lambda est valeur propre de A(une matrice carrée) si et seulement si PA(lambda) =0". J'ai noté PA le polynôme caractéristique de A.
Voilà la démonstration que j'ai, avec en gras et soulignée la partie que je ne comprends pas (je ne fais pas le lien avec la première phrase juste avant). Hormis ça, je comprends, mais bon, c'est le coeur du truc :/
"Un nombre lambda est une valeur propre de A s'il existe un vecteur colonne X non nul tel que AX=lambda*X. Cela revient exactement à dire que la matrice A - lambda*In n'est pas inversible donc que det(A-lambda*In)=0 c'est-à-dire PA(lambda) =0"
Quel est le lien?
Merci!
Bonsoir,
s'il existe X non nul tel que AX=\lambda X, alors en groupant d'un même côté de l'équation
(A-\Lambda I)X = 0
ça veut dire que X est dans le noyau de (A-\lambda I), donc que ce noyau n'est pas réduit à 0, donc que la matrice (A-\lambda I) n'est pas inversible (pas injective en particulier).
s'il existe X non nul tel que AX=\lambda X, alors en groupant d'un même côté de l'équation
(A-\Lambda I)X = 0
ça veut dire que X est dans le noyau de (A-\lambda I), donc que ce noyau n'est pas réduit à 0, donc que la matrice (A-\lambda I) n'est pas inversible (pas injective en particulier).
Salut,
Cela vient du résultat archi classique qui te dit que, si A est la matrice (carrée) d'un endomorphisme de E (e.v. de dim finie), il y a équivalence entre :
(1) A est bijective (vu comme l'application X->AX)
(2) A est injective (vu comme l'application X->AX)
(3) A est surjective (vu comme l'application X->AX)
(4) Ker(A)={0} (i.e. AX=0 => X=0)
(5) Im(A)=E (vu comme l'application X->AX)
(6) A est inversible
(7) det(A) est non nul
Ensuite, dire qu'il existe vecteur colonne X non nul tel que AX=lambda.X, équivaut à dire qu'il existe un vecteur non nul tel que (A-lambda.In)X=0, ce qui équivaut à dire que Ker(A-lambda.In) est non réduit à {0} ce qui équivaut à dire que det(A-lambda.In)=0.
EDIT : grilled...
Cela vient du résultat archi classique qui te dit que, si A est la matrice (carrée) d'un endomorphisme de E (e.v. de dim finie), il y a équivalence entre :
(1) A est bijective (vu comme l'application X->AX)
(2) A est injective (vu comme l'application X->AX)
(3) A est surjective (vu comme l'application X->AX)
(4) Ker(A)={0} (i.e. AX=0 => X=0)
(5) Im(A)=E (vu comme l'application X->AX)
(6) A est inversible
(7) det(A) est non nul
Ensuite, dire qu'il existe vecteur colonne X non nul tel que AX=lambda.X, équivaut à dire qu'il existe un vecteur non nul tel que (A-lambda.In)X=0, ce qui équivaut à dire que Ker(A-lambda.In) est non réduit à {0} ce qui équivaut à dire que det(A-lambda.In)=0.
EDIT : grilled...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
L.A. a écrit:Bonsoir,
s'il existe X non nul tel que AX=\lambda X, alors en groupant d'un même côté de l'équation
(A-\Lambda I)X = 0
ça veut dire que X est dans le noyau de (A-\lambda I), donc que ce noyau n'est pas réduit à 0, donc que la matrice (A-\lambda I) n'est pas inversible (pas injective en particulier).
1)Si l'endomorphisme (que représente ici A dans une certaine base) n'est pas injectif, il n'est par conséquent pas bijectif, et les différentes matrices qui peuvent le représenter (dont A ici) ne sont pas inversibles. C'est ça?
2)Je me permets une deuxième question de calcul, en lien avec le polynôme caractéristique. Même chose, en gras et souligné ce que je ne comprends pas.
"Deux matrices semblables ont le même polynôme caractéristique.
Preuve : soient A et B deux matrices carrées d'ordre n, P une matrice inversible d'ordre n, telles ques B =(P1*A*P (Pour que ce soit moins désagréable à lire, je note P1 la matrice inverse de P).
det(P1*A*P-XIn) = det(P*A*P1 - X*P*P1) = det(P*(A-XIn)*P1) = det(P)det(A-XIn)det(P1) = det(A-XIn)"
Je comprends qu'on "factorise" (c'est moche ce mot ici), mais de quel droit X*P*P1 devient-il P*X*P1 ? En gros, pourquoi y a t'il droit de commuter P et X ici?
Merci
Edit pour le 1) : Merci Ben314, j'avais perdu de vue ces équivalences. Celles-ci sont-elles valables pour les applications linéaires en général ?
Je veux bien de l'aide pour le 2) :hein:
1) oui, sachant qu'ici tout est plus simple puisqu'on a une base canonique, une matrice s'identifie vraiment à un endomorphisme.
2) Il faut garder à l'esprit que dans le polynôme caractéristique, X désigne un scalaire (indéterminé ou variable certes, mais un scalaire tout de même), et à ce titre il commute forcément avec toute matrice :
a(AB) = (aA)B = A(aB)
2) Il faut garder à l'esprit que dans le polynôme caractéristique, X désigne un scalaire (indéterminé ou variable certes, mais un scalaire tout de même), et à ce titre il commute forcément avec toute matrice :
a(AB) = (aA)B = A(aB)
L.A. a écrit:1) oui, sachant qu'ici tout est plus simple puisqu'on a une base canonique, une matrice s'identifie vraiment à un endomorphisme.
2) Il faut garder à l'esprit que dans le polynôme caractéristique, X désigne un scalaire (indéterminé ou variable certes, mais un scalaire tout de même), et à ce titre il commute forcément avec toute matrice :
a(AB) = (aA)B = A(aB)
Merci! Pour la 2), oui bien sûr, j'ai craqué, j'ai fait comme si c'était une matrice (vecteur colonne -_-"), et non un scalaire.
Pour ma question à Ben314 (savoir si ces équivalences sont vraies pour les applis linéaires en général), je ne parle évidemment pas des matrices inversibles et inverses (qui se doivent d'être carrées si j'ai bien compris). =>Edit : à moins qu'on ne travaille sur des applis linéaires entre des espaces E et F de mêmes dimensions ? Je me dis que ces applis, peuvent être représentées comme toute application avec une matrice, mais si elles sont bijectives, alors on peut leur trouver une matrice inverse...
Bonjour,
ce théorème n'est pas compliqué du tout; c'est la formulation qu'on t'a donnée qui le rend obscur;
je te donne un exemple en dimension 3:
soit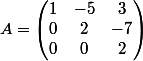 et
et 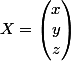 .
.
 , réel ou complexe est valeur propre de A ssi il existe un vecteur X non nul tel que:
, réel ou complexe est valeur propre de A ssi il existe un vecteur X non nul tel que:
X=0 Ker(A-\lambda Id)\ne 0)
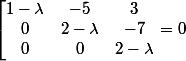
=(\lambda-1)(\lambda-2)^2=0)
Donc) est le polynôme caractéristique de A qui a donc deux valeurs propres, à savoir
est le polynôme caractéristique de A qui a donc deux valeurs propres, à savoir 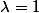 ou
ou 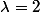 dont l'ordre de multiplicité est 2; donc A n'est pas forcément diagonalisable; pour le savoir tu dois déterminer la dimension de Ker(A-2Id) c'est à dire résoudre le système linéaire:
dont l'ordre de multiplicité est 2; donc A n'est pas forcément diagonalisable; pour le savoir tu dois déterminer la dimension de Ker(A-2Id) c'est à dire résoudre le système linéaire:
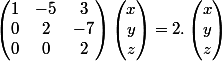
ce théorème n'est pas compliqué du tout; c'est la formulation qu'on t'a donnée qui le rend obscur;
je te donne un exemple en dimension 3:
soit
Donc
paquito a écrit:Bonjour,
ce théorème n'est pas compliqué du tout; c'est la formulation qu'on t'a donnée qui le rend obscur;
je te donne un exemple en dimension 3:
soitet
.
, réel ou complexe est valeur propre de A ssi il existe un vecteur X non nul tel que:
Doncest le polynôme caractéristique de A qui a donc deux valeurs propres, à savoir
ou
dont l'ordre de multiplicité est 2; donc A n'est pas forcément diagonalisable; pour le savoir tu dois déterminer la dimension de Ker(A-2Id) c'est à dire résoudre le système linéaire:
Ok merci! J'ai bien compris ça
Petite question :Ben314 a écrit :
"Salut,
Cela vient du résultat archi classique qui te dit que, si A est la matrice (carrée) d'un endomorphisme de E (e.v. de dim finie), il y a équivalence entre :
(1) A est bijective (vu comme l'application X->AX)
(2) A est injective (vu comme l'application X->AX)
(3) A est surjective (vu comme l'application X->AX)
(4) Ker(A)={0} (i.e. AX=0 => X=0)
(5) Im(A)=E (vu comme l'application X->AX)
(6) A est inversible
(7) det(A) est non nul
"
Ceci n'est valable que pour les endomorphismes ou pour toute application linéaire? Je pensais que c'était valable pour toute application linéaire entre deux espaces de même dimension.
L.A. a écrit:1) oui, sachant qu'ici tout est plus simple puisqu'on a une base canonique, une matrice s'identifie vraiment à un endomorphisme.
2) Il faut garder à l'esprit que dans le polynôme caractéristique, X désigne un scalaire (indéterminé ou variable certes, mais un scalaire tout de même), et à ce titre il commute forcément avec toute matrice :
a(AB) = (aA)B = A(aB)
bonjour,
je suis pas trop d'accord ni avec (1), ni avec (2).
tu connais les arguments qui vont "contre" mieux que moi.
Bizarre a écrit:Ok merci! J'ai bien compris ça
Petite question :Ben314 a écrit :
"Salut,
Cela vient du résultat archi classique qui te dit que, si A est la matrice (carrée) d'un endomorphisme de E (e.v. de dim finie), il y a équivalence entre :
(1) A est bijective (vu comme l'application X->AX)
(2) A est injective (vu comme l'application X->AX)
(3) A est surjective (vu comme l'application X->AX)
(4) Ker(A)={0} (i.e. AX=0 => X=0)
(5) Im(A)=E (vu comme l'application X->AX)
(6) A est inversible
(7) det(A) est non nul
"
Ceci n'est valable que pour les endomorphismes ou pour toute application linéaire? Je pensais que c'était valable pour toute application linéaire entre deux espaces de même dimension.
Qu'est ce que ça veut dire "endomorphisme"? Ben sait ce qu'il dit, tu peux lui faire confiance! Moi je ne fais qu'illustrer son cours magistral!
salut
il semble évident qu'il n'existe pas de bijection entre deux espaces vectoriels qui n'ont pas la même dimension (finie)
si f : E --> F
si Dim(E) < Dim(F) alors f ne peut pas être surjective
si Dim(E) > Dim(F) alors f ne peut pas être injective
(il suffit de considérer une base de E et de fixer leur images par f)
il semble évident qu'il n'existe pas de bijection entre deux espaces vectoriels qui n'ont pas la même dimension (finie)
si f : E --> F
si Dim(E) < Dim(F) alors f ne peut pas être surjective
si Dim(E) > Dim(F) alors f ne peut pas être injective
(il suffit de considérer une base de E et de fixer leur images par f)
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
zygomatique a écrit:salut
il semble évident qu'il n'existe pas de bijection entre deux espaces vectoriels qui n'ont pas la même dimension (finie)
si f : E --> F
si Dim(E) Dim(F) alors f ne peut pas être injective
(il suffit de considérer une base de E et de fixer leur images par f)
Pour être un petit plus précis, il n'existe pas d'application linéaire bijective
(Il y a des bijection de R dans R^2, mais ce ne sont pas des application linéaires)
mathelot a écrit:bonjour,
je suis pas trop d'accord ni avec (1), ni avec (2).
tu connais les arguments qui vont "contre" mieux que moi.
Ah bon ?
1) Est-ce que étudier des matrices carrées ce n'est pas étudier des endomorphismes de R^n, et est-ce que R^n n'est pas muni d'une base canonique qui fait qu'il n'y a pas d'ambiguité ?
2) Si K est un corps, il faut bien comprendre la différence entre M_n(K[X]) et "M_n(K)[X]" : je ne suis même pas sur que la seconde écriture puisse exister vu que M_n(K) est un anneau non commutatif, par contre, la première est de la forme M_n(R) c'est à dire que c'est l'anneau des matrices à coefficients dans un anneau R (commutatif ou pas), il n'y a aucun problème pour le définir (bien sûr les éléments inversibles de cet anneau sont moins nombreux).
Le polynôme caractéristique P_A d'une matrice A dans M_n(K) est le déterminant d'une matrice B = (A-XI) vue comme matrice à coefficients dans l'anneau K[X], la matrice B est donc dans M_n(K[X]) et son déterminant P_A dans K[X].
Moralité : Mon corps de base K devient un anneau de base K[X], j'ai simplement adjoint aux scalaires un nouveau scalaire indéterminé X.
zygomatique a écrit:bien sur queexiste ....
l'objet X pouvant aussi bien représenter un scalaire (de K) qu'une matrice (de M_n(K))
...
Oui mais écrire un monôme sous la forme AX^n n'aurait pas d'intérêt à cause de la non commutativité, il faudrait envisager AX^{n_1}BX^{n_2}C... est-ce que ça se fait, je ne sais pas.
ça, c'est pas terrible...Bizarre a écrit:Edit pour le 1) : Merci Ben314, j'avais perdu de vue ces équivalences. Celles-ci sont-elles valables pour les applications linéaires en général ?
Si tu veut comprendre les truc en math, (en particulier en algèbre linéaire), c'est on ne peut plus utile que les "pré-requis" soit bien acquis, sinon... tu es mal..
Sinon, une autre "piqure de rappel" concernant ta question sur la suite d'équivalences que j'ai donné :
Elle sont valables pour tout endomorphisme (i.e. application linéaire de E->E) sur un e.v. de dim finie et même pour tout application linéaire de E->F où E et F sont de même dimension.
Si E et F sont de dimension différentes, c'est tout complètement faux, mais d'un autre coté, un truc à savoir absolument (vu qu'on l'utilise archi super souvent sans même le dire), c'est le théorème dit "du rang" :
Si f:E->F est linéaire avec E et F de dim fini, alors dim(Ker(f))+dim(Im(f))=dim(E)
Et tu déduit immédiatement de cette égalité que :
- Si dim(E)dim(F) on s'en fout de pas pouvoir calculer de déterminant dans ce cas là, vu qu'il n'y a nulle besoin de "déterminer" si f est bijective ou pas : elle ne l'est forcément pas.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
On peut parler un peu des applications linéaires en dimension infinie ou tu n'as plus de matrices.
Considérons le R-espace vectoriel des polynômes à coefficients réels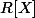 et l'endomorphisme
et l'endomorphisme
défini par par->\Phi (P(x)=xP(x))) ;
;  n'est clairement pas bijective puisque les
n'est clairement pas bijective puisque les
polynômes constants n'ont pas d'antécédent et pourtant=0) , mais
, mais \ne <br /><br />R[X]) ; l'intérêt de
; l'intérêt de  est que si l'on note
est que si l'on note
=\bigsum_{i=0}^{n}a_ix^i) , on utilise souvent la norme
, on utilise souvent la norme ||=sup(a_i))
et relativement à cette norme, est une isométrie non-bijective alors qu'en
est une isométrie non-bijective alors qu'en
dimension finie, toute isométrie est bijective.
Tout ça pour te montrer qu'il ne fallait pas prendre l'habitude de confondre matrices carrées et
applications linéaires comme te l'a dit Ben.
Considérons le R-espace vectoriel des polynômes à coefficients réels
défini par par
polynômes constants n'ont pas d'antécédent et pourtant
et relativement à cette norme,
dimension finie, toute isométrie est bijective.
Tout ça pour te montrer qu'il ne fallait pas prendre l'habitude de confondre matrices carrées et
applications linéaires comme te l'a dit Ben.
Faire gaffe quand même que ça dépend de la définition qu'on prend de "isométrie".paquito a écrit:...alors qu'en dimension finie, toute isométrie est bijective.
Pour certains auteurs, f:(x,y)->(x,y,0) de R^2 dans R^3 est considéré comme une isométrie (on a trivialement ||f(X)||=||X||) et elle n'est clairement pas bijective !!!
Donc perso, je préfèrerais écrire qu'une isométrie est trivialement injective, (en dimension finie ou pas) vu que f(X)=0 => ||X||=||f(X)||=0 puis que, en dimension finie, si les espaces de départ et d'arrivé ont même dimension, ça suffit à prouver la bijectivité de f.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Salut Ben,
Faut vraiment être vicieux pour envisager une isométrie qui ne conserve pas la dimension; en tout cas c'est pas admis à l'agrégation; parler de restriction d'une rotation vectorielle en dim 3 au plan vectoriel par rapport à l'axe de la rotation, là pas de problème; mais de là à qualifier isométrie l'application de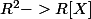 qui à (a; b) associe (0; 0; a ; b; 0; 0; .......,0,....) je trouve ça difficilement défendable sur le plan pédagogique, donc je n'utiliserait pas cette définition, même si a priori elle est correcte. Enfin, ça sert à quoi??
qui à (a; b) associe (0; 0; a ; b; 0; 0; .......,0,....) je trouve ça difficilement défendable sur le plan pédagogique, donc je n'utiliserait pas cette définition, même si a priori elle est correcte. Enfin, ça sert à quoi??
Faut vraiment être vicieux pour envisager une isométrie qui ne conserve pas la dimension; en tout cas c'est pas admis à l'agrégation; parler de restriction d'une rotation vectorielle en dim 3 au plan vectoriel par rapport à l'axe de la rotation, là pas de problème; mais de là à qualifier isométrie l'application de
22 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
