Bonjour,
J’ai un exercice à faire où je n’y arrive pas trop.
Voici l’énoncé :
Soit la fonction défini sur [0;+infini] par f(x)= racine(X)/x+1
1) monter que f est dérivable sur ]0;+infini[ et calculer f'(x)
2) étudier les variations de f et en déduire que pour tout réel positif x on a 0≤racine(x)≤(x+1):2
3) montrer que pour tout réel strictement posotif x on a f(x)≤1:racine(x). En déduire un intervalle sur lequel on a f(x)≤10^-2
1) je l’ai fait
2) est ce que ca fait - (1/2 racine(x) / x^2+2x+1) ?
Exercice dérivée
9 messages
- Page 1 sur 1
Re: Exercice dérivée
Excusez moi, f’(x) c’est le résultat que j’ai mis à la 2. Est ce que vous pouvez me confirmer que c’est ça ? Merci
Re: Exercice dérivée
Bonjour ,
Je ne comprends pas pourquoi au dessus de la fraction, c’est 1-x? Avec mes calculs, je trouve la même chose en bas mais je trouve -1 en haut
Merci
Je ne comprends pas pourquoi au dessus de la fraction, c’est 1-x? Avec mes calculs, je trouve la même chose en bas mais je trouve -1 en haut
Merci
Re: Exercice dérivée
donne ce que tu trouves (si tu sais pas faire en latex, mets des espaces et des parenthèses), la fraction a été un peu modifiée pour faire disparaître des racines.
Re: Exercice dérivée
Difficile de deviner d'où vient ton erreur au numérateur. Tout ce que je peux te dire, c'est de reprendre ton calcul méthodiquement :
1/Ecrire la fonction f sous la forme u/v : identifier ce qu'est u, ce qu'est v
2/Calculer les dérivées de u et de v
3/Ecrire les 4 fonctions u, v, u' et v' les unes en dessous les autres, ou à minima encadrer les 4 fonctions sur ton brouillon : cela te permettra de te référer plus facilement à ces résultats dans l'application de la formule de la dérivée d'un quotient de fonctions
4/Appliquer la formule de la dérivée d'un quotient de fonctions :
a) d'abord faire le calcul du numérateur,
b) puis faire le calcul du dénominateur,
c) Faire le quotient numérateur/dénominateur
Remarque : calculer séparément le numérateur et le dénominateur est loin d'être une obligation, mais cela te permet d'éviter les traits de fraction multiples qui peuvent être une source d'erreurs.
C'est à toi de trouver ton erreur, on ne progresse que comme cela en calcul
1/Ecrire la fonction f sous la forme u/v : identifier ce qu'est u, ce qu'est v
2/Calculer les dérivées de u et de v
3/Ecrire les 4 fonctions u, v, u' et v' les unes en dessous les autres, ou à minima encadrer les 4 fonctions sur ton brouillon : cela te permettra de te référer plus facilement à ces résultats dans l'application de la formule de la dérivée d'un quotient de fonctions
4/Appliquer la formule de la dérivée d'un quotient de fonctions :
a) d'abord faire le calcul du numérateur,
b) puis faire le calcul du dénominateur,
c) Faire le quotient numérateur/dénominateur
Remarque : calculer séparément le numérateur et le dénominateur est loin d'être une obligation, mais cela te permet d'éviter les traits de fraction multiples qui peuvent être une source d'erreurs.
C'est à toi de trouver ton erreur, on ne progresse que comme cela en calcul
Re: Exercice dérivée
Bonjour,
Merci J’ai enfin réussi le calcul.
Pour la 2, j’ai fait les variations de f mais je ne vois pas le rapport entre ca et l’encadrement à déduire.
Merci
Merci J’ai enfin réussi le calcul.
Pour la 2, j’ai fait les variations de f mais je ne vois pas le rapport entre ca et l’encadrement à déduire.
Merci
Re: Exercice dérivée
Salut !
Si tu observes bien l'expression de) et ce qu'on te demande de montrer, tu devrais remarquer que cela revient à montrer que pour tout
et ce qu'on te demande de montrer, tu devrais remarquer que cela revient à montrer que pour tout 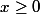 , on a
, on a  \le \frac 1 2) .
.
Le fait que \ge 0) , pour tout
, pour tout 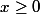 , est évident par hypothèse de l'énoncé : la fonction
, est évident par hypothèse de l'énoncé : la fonction  est définie sur
est définie sur  par
par = \frac{\sqrt x}{x+1}) (un quotient de deux réels positifs dont le dénominateur ne s'annule pas est toujours positif).
(un quotient de deux réels positifs dont le dénominateur ne s'annule pas est toujours positif).
Reste à montrer que pour tout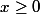 , on a
, on a  \le \frac 1 2) , je te laisse le déduire compte tenu des variations de
, je te laisse le déduire compte tenu des variations de  .
.

Si tu observes bien l'expression de
Le fait que
Reste à montrer que pour tout
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
