Noyau
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 25 Déc 2017, 18:14
par mehdi-128 » 25 Déc 2017, 18:14
Bonjour,
On se place dans

.
Soit Q une matrice symétrique réelle à termes strictement positifs telle que si c est un vecteur de

on a :
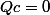
On a aussi si on note
)
le vecteur c auquel on a ôté la ligne j on a la propriété suivante :
le vecteur
)
est colinéaire à un vecteur noté
)
à composantes strictement positives.
On peut écrire vu que
)
est non nul :
=\lambda_j m(j))
Je dois montrer que c=0
Je suis parti de :
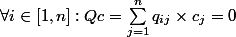
Et là je bloque
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 26 Déc 2017, 00:45
par infernaleur » 26 Déc 2017, 00:45
Salut,
(j’arrive pas à écrire des vecteurs colonnes donc j'écrirais en lignes)
Voila une piste :
On pose
=(m_1,...,m_{j-1},m_{j+1},...,m_n))
on pose
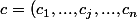)
Par hypothèse comme
=\lambda_j m(j))
on a :
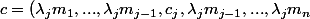)
Donc la somme que tu as écrites se réécrit :
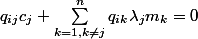
Donc tu as
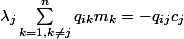
Comme les
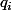
sont strictement positif et les
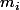
aussi, il en résulte que
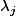
et
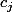
sont de signe opposés
En repartant de
=\lambda_j m(j))
on a en supposant que
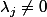
=\frac{c(j)}{\lambda_j})
, or comme
)
est strictement positif on aurait donc que
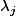
et tout les

pour i différent de j sont de mêmes signes.
Si on refait la même chose en enlevant une autre ligne au vecteur c ( a la place du vecteur j ) on pourrait peut-être arriver à une contradiction.
(je continuerais demain)
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 26 Déc 2017, 11:40
par arnaud32 » 26 Déc 2017, 11:40
Q:
1 1
1 1
c=
1
-1
Q, est symetrique reelle a coefficients positifs et Qc= 0
c verifie la propriete avec m(j)= 1 et, L1=-1 et L2=1
or c n'est pas nul
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 04 Jan 2018, 17:11
par mehdi-128 » 04 Jan 2018, 17:11
Bien vu Arnaud j'ai oublié de préciser la matrice Q !
On a :
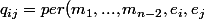)
avec (i,j) dans [1,n]
Pour
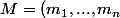 \in M_{n,n} (R))
on définit son permanent de
)^n)
dans

par :
=\sum_{\sigma \in \mathfrak{S}_n}m_{1 \sigma(1)} \times ... \times m_{n \sigma(n)})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités