Inégalité
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 18 Aoû 2017, 21:38
par mehdi-128 » 18 Aoû 2017, 21:38
Bonsoir,
Soit x un réel strictement positif. Soit n un entier supérieur ou égal à 2.
J'ai beaucoup de souci pour le passage à la fonction : x --> u^x dans les inégalités.
J'ai k un entier compris entre 1 et n-1 et j'ai :
} \geq \frac{4}{n^2} \geq 0)
J'aimerais appliquer la puissance x à l'inégalité mais je sais pas si ça va changer le signe de l'inégalité ou pas.
-
NumHéroBis
- Membre Naturel
- Messages: 20
- Enregistré le: 23 Juil 2017, 16:46
-
 par NumHéroBis » 18 Aoû 2017, 21:44
par NumHéroBis » 18 Aoû 2017, 21:44
Salut, la fonction
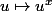
est-elle croissante sur
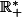
(l'ensemble des réels strictement positifs) ?
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 18 Aoû 2017, 22:04
par mehdi-128 » 18 Aoû 2017, 22:04
Si je note :
=u^x)
On a :
= xu^{x-1})
En x=1 :
=x \geq 0)
Si x>1 :
=xu^{|x-1|} \geq 0)
f est croissante sur ]0,+infini[
Si x<1 :
=\frac{x}{u^{|x-1|}} \geq 0)
f est croissante sur ]0,+infini[
C'est correct ?
-
NumHéroBis
- Membre Naturel
- Messages: 20
- Enregistré le: 23 Juil 2017, 16:46
-
 par NumHéroBis » 18 Aoû 2017, 22:10
par NumHéroBis » 18 Aoû 2017, 22:10
Pour tout
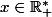
,
 \ge 0)
car x est strictement positif et u l'est aussi.
Donc f' est positive sur les réels positifs. Qu'est-ce que l'on peut en conclure ?
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 18 Aoû 2017, 22:55
par mehdi-128 » 18 Aoû 2017, 22:55
Si f est croissante sur R+* alors on peut appliquer la fonction f à l'inégalité sans changer le signe de l'inégalité :
} \geq \frac{4}{n^2} \geq 0)
Donc :
)^x} \geq \frac{4^x}{n^{2x}})
-
cailloux1
- Membre Naturel
- Messages: 40
- Enregistré le: 18 Nov 2013, 21:44
-
 par cailloux1 » 19 Aoû 2017, 08:42
par cailloux1 » 19 Aoû 2017, 08:42
Bonjour,
Beaucoup de confusions:
J'ai beaucoup de souci pour le passage à la fonction : x --> u^x dans les inégalités...
Si je note :
=u^x)
C' est une fonction de

ou de

?
NumHéroBis a écrit:Pour tout
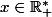
,
 \ge 0)
car x est strictement positif et u l'est aussi.
et si c'est une fonction de

, ses variations dépendent de la place de

par rapport à 1
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 19 Aoû 2017, 17:06
par mehdi-128 » 19 Aoû 2017, 17:06
C'est une fonction de u mais le x est une variable fixée....
x est un réels strictement positif et je veux appliquer la puissance x à mon inégalité.
C'est f'(u) qui est positif on s'est un peu mélangé.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
