l'argument " vu la forme .. " n'est bien sur pas une preuve, juste un indice si cherche dans cette voie, sinon il ya celle proposée par nightmare
Ps : expliquer quoi ?
Inégalité sur les coefficients d'un polynôme
33 messages
- Page 2 sur 2 - 1, 2
Je me demande si on ne peut pas faire une récurrence sur le degré des polynômes.
Pour on a
on a 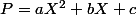 et
et  admet deux racines réelles distinctes si
admet deux racines réelles distinctes si  et on a
et on a  donc ça marche.
donc ça marche.
On suppose que la propriété est vraie pour tous les polynômes de degré qui ont
qui ont  racines réelles distinctes.
racines réelles distinctes.
Soit un polynôme de degré
un polynôme de degré  qui admet
qui admet  racines réelles distinctes. On suppose que
racines réelles distinctes. On suppose que  est racine de
est racine de  (si ce n'est pas le cas, on considère pour
(si ce n'est pas le cas, on considère pour  racine
racine  =P\(X-\alpha\)) ).
).
On écrit . On considère
. On considère  .
.  admet
admet  racines réelles distinctes et est un polynôme de degré
racines réelles distinctes et est un polynôme de degré  . On pose
. On pose  . L'hypothèse de récurrence assure que pour tout
. L'hypothèse de récurrence assure que pour tout  on a
on a  c'est à dire que pour tout
c'est à dire que pour tout  on a
on a  donc pour tout
donc pour tout  on a
on a  .
.
Il reste à montrer que . On a
. On a 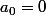 donc il suffit de voir que
donc il suffit de voir que  , ce qui est le cas sinon
, ce qui est le cas sinon  serait racine de
serait racine de  ce qui est exclu.
ce qui est exclu.
Pour
On suppose que la propriété est vraie pour tous les polynômes de degré
Soit
On écrit
Il reste à montrer que
Ben314 a écrit:Le petit problème, c'est que, quand tu passe deà
ben ça modifie sacrément les coeffs du polynôme...
Oui, il faut que je montre que le lien entre les anciens et les nouveaux coefficient (plus compliqué que ce que je croyais) permet de conserver la propriété que l'on veut montrer. Je me penche là-dessus.
Perso, avec les polynômes symétriques élémentaires, je suis pas arrivé à grand chose...
Par contre, avec l'indic de Nightmare, ça se fait de façon relativement simple...
La "méthode Girdav" parrait bonne, mais j'ai peur que le lien entre les coeffs de P et de \tilde{P} soit un peu dissuasif...
Par contre, avec l'indic de Nightmare, ça se fait de façon relativement simple...
La "méthode Girdav" parrait bonne, mais j'ai peur que le lien entre les coeffs de P et de \tilde{P} soit un peu dissuasif...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Perso, avec les polynômes symétriques élémentaires, je suis pas arrivé à grand chose...
Par contre, avec l'indic de Nightmare, ça se fait de façon relativement simple...
La "méthode Girdav" parrait bonne, mais j'ai peur que le lien entre les coeffs de P et de \tilde{P} soit un peu dissuasif...
c'est une simple inegalité pourtant
Je ne connais pas ce que represente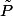 ..
..
J'imagine ... mais je ne sais pas manipuler les polynômes symétriques élémentaires. J'ai essaye de chercher une relation entre sigma(k-1) et sigma (k) mais j'ai pas trouvé .. (pour l'instant) mais j'aimerais bien bien savoir s'il existe des relations assez intéressante , exploitable.
windows7 a écrit:et pourtant le resultat en decoule ..
J'imagine ... mais je ne sais pas manipuler les polynômes symétriques élémentaires. J'ai essaye de chercher une relation entre sigma(k-1) et sigma (k) mais j'ai pas trouvé .. (pour l'instant) mais j'aimerais bien bien savoir s'il existe des relations assez intéressante , exploitable.
Ben314 a écrit:Perso, avec les polynômes symétriques élémentaires, je suis pas arrivé à grand chose...
Par contre, avec l'indic de Nightmare, ça se fait de façon relativement simple...
La "méthode Girdav" parrait bonne, mais j'ai peur que le lien entre les coeffs de P et de \tilde{P} soit un peu dissuasif...
t'as regardé du coté des forume de newton ?
Je poste une solution, très très largement suggérée par Ben :
On considère le polynôme P'/P . Si on écrit=\lambda (X-x_1)...(X-x_n)) grâce au fait que avec
grâce au fait que avec  des fonctions dérivables
des fonctions dérivables =\bigsum_{k=1}^{n}f_1...f_i...f_n)
Ainsi en identifiant P a sa fonction polynômiale on a après simplification pour tout X:
}{P(X)}=\Bigsum_{k=1}^n\frac{1}{(X-x_k})
En dérivant on a facilement le Lemme suggéré par nightmare. Par suite, en prenant pour x=0 on obtient
Le théorème de Rolle nous donne que P' a n-1 racines réelles, ainsi on peut ré-appliquer le Lemme à P', P'' et P''' pour avoir les inégalités sur les coefficients suivants. Par récurrence on conclu.
On considère le polynôme P'/P . Si on écrit
Ainsi en identifiant P a sa fonction polynômiale on a après simplification pour tout X:
En dérivant on a facilement le Lemme suggéré par nightmare. Par suite, en prenant pour x=0 on obtient
Le théorème de Rolle nous donne que P' a n-1 racines réelles, ainsi on peut ré-appliquer le Lemme à P', P'' et P''' pour avoir les inégalités sur les coefficients suivants. Par récurrence on conclu.
33 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
