Dérivée

[oasis11]

Bonjour à tous,

Après plusieurs heures de réflexion sur une dérivée qui m'avait l'air plutôt simple, je décide donc de solliciter votre aide :

f(x) = {x^3+2x^2}/{x^2+2x+1}

J'utilise bien sûr la formule {u}/{v} mais après je n'y arrive pas du tout.

Merci d'avance pour ceux qui m'aideront.

[Black Jack]

u = x³+2x² --> u' = 3x² + 4x
v = x² + 2x + 1 --> v' = 2x + 2

f'(x) = (u'.v - u.v')/v² = ...

[oasis11]

Merci pour votre réponse rapide

J'ai appliqué cette formule et je me trouve avec un résultat différent de celui proposé

Je dois démontrer que f est égale à f'(x) = {x^3+3x^2-4x}/{x+1}^3

Je me retrouve avec cela : f'(x)= {-x^4-4x^3+x^2+4x}/{x+1}^2

[capitaine nuggets]

Salut !

Vérifie tes calculs. Sans calculs intermédiaires, il nous sera difficile de t'aider davantage

[zygomatique]

salut

depuis le collège je sais que ....

[oasis11]

Salut zygomatique. J'ai également utilisé cette formule mais après je ne sais pas comment faire.

f(x)=
f(x) =

[samoufar]

Bonjour,

Pour simplifier un peu plus les calculs, tu peux aussi remarquer que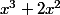 est à peu de choses près .

[Razes]

laisser groupée car il y aura des simplification.

[oasis11]

En suivant vos conseils voilà ce que j'ai :

f(x) =

En supprimant (x+1) au dénominateur et au numérateur j'obtiens cela :

f(x) =

Mais après je continue à bloquer.

[zygomatique]

[oasis11]

Merci zygomatique

Que c'est dur de reprendre les maths (comme quoi avoir son bac...)

Bref merci à tous pour votre aide, c'est super !

[samoufar]

Bonjour,

On peut simplifier les calculs :





en utilisant le fameux .

L'avantage est d'une part que cette expression est décomposée en éléments simples et d'autre part que les calculs intermédiaires de dérivées sont simples (on ne s'embrouille pas ).

[zygomatique]

ouais enfin ... le calcul d'une dérivée a souvent pour objectif d'étudier son signe pour obtenir les variations de f ...

j'y avais bien pensé mais il faudra réduire au même dénominateur pour étudier le signe ...

[oasis11]

Hello les amis !

J'ai encore un petit problème avec une autre dérivée (décidément...)

f(x) =

Bien entendu c'est encore de la forme (u/v)

f(x) =

Et je trouve cela :

f(x) =

Mais sachant que le résultat est f(x)= je me vois mal embarqué.

[samoufar]

Bonjour,

Tu as bien

Simplifie ta fraction au maximum, factorise par et développe ce qui reste au numérateur

Au fait, tu es sûr que ce n'est pas du au dénominateur dans la solution que tu donnes ?

[zygomatique]

salut

ne pas confondre f et f' ...

il y a une erreur de simplification ...

[oasis11]

Je viens de trouver. Effectivement il y a une erreur c'est bien (x+1)^3 au dénominateur

f(x)=
f(x)=
f(x)=

Merci pour le (x-2)^2 en facteur

[samoufar]

Pas de problème

C'est OK pour ta solution. Juste un détail (qui a son importance), tu es en train de déterminer f' et non f