équations/ inéquations
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries

-
laetidom
- Habitué(e)
- Messages: 5720
- Enregistré le: 16 Déc 2013, 16:15
-
 par laetidom » 29 Fév 2016, 15:24
par laetidom » 29 Fév 2016, 15:24
lu2pm a écrit:sisi nous avons fait que les tableaux de signes , pour le tableau j'ai fait une erreur?
http://www.cjoint.com/c/FBDoxU1uNU7 (qui correspond aux graphes que je t'ai déjà fait parvenir . . .)
-
lu2pm
- Membre Naturel
- Messages: 15
- Enregistré le: 24 Fév 2016, 16:08
-
 par lu2pm » 29 Fév 2016, 15:27
par lu2pm » 29 Fév 2016, 15:27
laetidom a écrit: lu2pm a écrit:http://www.cjoint.com/c/FBDn5TLbLKe je ne suis pas du tout sure de moi habituellement nous ne faisons pas des tableaux dans ce genre, sur le sujet la prof nous demande de résoudre graphiquement en expliquant la méthode puis de retrouver par le calcul , elle nous demande qu'à la fin de tracer la droite d'équation y=x
Es-tu sûre des signes de la dernière ligne ?Si tu corrige (
http://www.cjoint.com/c/FBDoxU1uNU7 ), le tableau de signes t'indique seulement que :
http://www.cjoint.com/c/FBDordxQtD7 , es-tu d'accord ? . . .
ah oui effectivement merci beaucoup
-
lu2pm
- Membre Naturel
- Messages: 15
- Enregistré le: 24 Fév 2016, 16:08
-
 par lu2pm » 29 Fév 2016, 15:29
par lu2pm » 29 Fév 2016, 15:29
laetidom a écrit:Aide pour le B.2) :
http://www.cjoint.com/c/FBDn6W8VU17Je suis d'accord, ce n'est pas un tableau de variations qui est demandé mais tu me dis que ce n'ai pas un tableau de signes non plus ?
peux-tu me scaner le genre de tableau que la prof vous demande ?
merci beaucoup pour l'aide, cela correspond bien a f(x)=9/4?

-
laetidom
- Habitué(e)
- Messages: 5720
- Enregistré le: 16 Déc 2013, 16:15
-
 par laetidom » 29 Fév 2016, 15:30
par laetidom » 29 Fév 2016, 15:30
donc B.1 fait,
le B.2 je t'ai montré graphiquement pour le 9/4, le 0 est encore plus facile,
Modifié en dernier par
laetidom le 29 Fév 2016, 15:33, modifié 1 fois.

-
laetidom
- Habitué(e)
- Messages: 5720
- Enregistré le: 16 Déc 2013, 16:15
-
 par laetidom » 29 Fév 2016, 15:31
par laetidom » 29 Fév 2016, 15:31
lu2pm a écrit: laetidom a écrit:Aide pour le B.2) :
http://www.cjoint.com/c/FBDn6W8VU17Je suis d'accord, ce n'est pas un tableau de variations qui est demandé mais tu me dis que ce n'ai pas un tableau de signes non plus ?
peux-tu me scaner le genre de tableau que la prof vous demande ?
merci beaucoup pour l'aide, cela correspond bien a f(x)=9/4?
oui, il te reste à déterminer
par le calcul ( dernière question du B.2) les solutions de l'égalité, c'est-à-dire les coordonnées du (des) point(s) d'intersection . . .
avec le calcul, tu va arriver à une équation du second degré à résoudre :
un
exemple de résolution niveau seconde :


^2 - (\frac{3}{4})^2 - 2 = 0)
^2 - (\frac{23}{16})^2 = 0)
^2 - (\frac{\sqrt{23}}{4})^2 = 0)
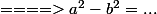
Modifié en dernier par
laetidom le 29 Fév 2016, 17:14, modifié 1 fois.
-
lu2pm
- Membre Naturel
- Messages: 15
- Enregistré le: 24 Fév 2016, 16:08
-
 par lu2pm » 29 Fév 2016, 16:22
par lu2pm » 29 Fév 2016, 16:22
c'est la premiere fois que je vois une équation du second degré, par contre comment avez vous trouvé le 2x²-3x-4 du départ?

-
laetidom
- Habitué(e)
- Messages: 5720
- Enregistré le: 16 Déc 2013, 16:15
-
 par laetidom » 29 Fév 2016, 17:13
par laetidom » 29 Fév 2016, 17:13
lu2pm a écrit:c'est la premiere fois que je vois une équation du second degré, par contre comment avez vous trouvé le 2x²-3x-4 du départ?
As-tu obtenu une équation du second degré dans ton calcul (cas du 9/4) ? . . .
2x²-3x-4 était un exemple, normalement tu dois tomber sauf erreur de ma part sur 8x² -24x +18 = 0 que tu résous avec la méthode décrite précédemment, compris ? . . .
donc, questions :
1) As-tu obtenu une équation du second degré dans ton calcul (cas du 9/4) ? . . .
2) Si oui, peux-tu la résoudre avec la méthode décrite précédemment ?
-
lu2pm
- Membre Naturel
- Messages: 15
- Enregistré le: 24 Fév 2016, 16:08
-
 par lu2pm » 29 Fév 2016, 17:46
par lu2pm » 29 Fév 2016, 17:46
a=8 , b = -24 et c = 18
Δ = b² - 4ac = (-24)² − 4×8×18 = 0
Δ = 0 alors l'équation 8x² − 24x + 18 = 0 admet une solution réélle double -b/2a
-b/2a = 24/16 = 3/2
= 8(x − 3/2)²
8x² − 24x + 18 ≥ 0 pour tout réel, car a = 8 > 0
j'ai obtenu ce résultat avec votre équation, mais je n'arrive pas a comprendre comment vous avez fait pour la trouver

-
laetidom
- Habitué(e)
- Messages: 5720
- Enregistré le: 16 Déc 2013, 16:15
-
 par laetidom » 29 Fév 2016, 20:47
par laetidom » 29 Fév 2016, 20:47
lu2pm a écrit:a=8 , b = -24 et c = 18
Δ = b² - 4ac = (-24)² − 4×8×18 = 0
Δ = 0 alors l'équation 8x² − 24x + 18 = 0 admet une solution réélle double -b/2a
-b/2a = 24/16 = 3/2
= 8(x − 3/2)²
===> donc S = {

}
que tu retrouve ici : http://www.cjoint.com/c/FBDn6W8VU178x² − 24x + 18 ≥ 0 pour tout réel, car a = 8 > 0
j'ai obtenu ce résultat avec votre équation, mais je n'arrive pas a comprendre comment vous avez fait pour la trouver
B.2résoudre graphiquement en expliquant la méthode les équations : a) f( x) =0 ; b) f( x)=9/4
retrouver par le calcul = \frac{2x^2+3x}{4x-2} = \frac{9}{4})
(2x²+3x).4 = (4x-2) .9
8x² + 12x = 36x -18
8x² -36x +12x + 18 = 0

On aurait pu faire aussi :
 = \frac{2x^2+3x}{4x-2} - \frac{9}{4} = 0)
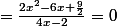
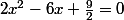
-
lu2pm
- Membre Naturel
- Messages: 15
- Enregistré le: 24 Fév 2016, 16:08
-
 par lu2pm » 29 Fév 2016, 21:27
par lu2pm » 29 Fév 2016, 21:27
encore merci pour votre grande aide, bonne soirée!

-
laetidom
- Habitué(e)
- Messages: 5720
- Enregistré le: 16 Déc 2013, 16:15
-
 par laetidom » 01 Mar 2016, 11:03
par laetidom » 01 Mar 2016, 11:03
lu2pm a écrit:encore merci pour votre grande aide, bonne soirée!
Ce fût un plaisir !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
} que tu retrouve ici : http://www.cjoint.com/c/FBDn6W8VU17