Incompréhension | Triangles : 2 = √2 ?!

[Kakemo]

Bonsoir m'sieurs les matheux ! :we:
Je post ici pour vous poser une question à laquelle je ne peux pas répondre...
En fait, ça ressemblerait à une sorte de paradoxe-énigme que je n'arrive pas à résoudre. :hum: Ainsi, après avoir torturé mes pauvres neurones, je viens vous supplier de réserver le même traitement aux vôtres :') (si si, c'est sérieux).

Allons, j'arrête de tourner en (x-h)²+(y-k)²=r² (hihi blague pourrie) et je pose la question...
Voilà, tout à l'heure je tombe sur un triangle ABC rectangle et isocèle en A. AB = 1.
Le problème est là : en calculant l'hypoténuse (CB je rappelle) avec une application toute bête de Pythagore je tombe sur :
CB² = AB² + BC²
CB² = 1² + 1²
CB² = 1+1
CB = (;)2)
Maintenant je place E, milieu de [AC] puis F, milieu de [AB]. Ensuite je place le point M, projeté de E sur [CB] selon le vecteur (AF->).
Alors CE+EM+MF+FB=CA+AB=2
Or si je place E', milieu de [CE], F', milieu de [FB], G, milieu de [EM], H, milieu de [MF], M', projeté de E' sur [CB] selon le vecteur (FF'->), M", projeté de F' sur [CB] selon le vecteur (EE'->) alors CE'+E'M'+M'G+GM+MH+HM"+M"F'+F'B=CA+AB=2.
(Pour la plupart il va falloir faire un schéma pour bien visualiser là... Moi je n'en ai pas fait, j'espère ne pas m'être trompé... Ce serait... Ballot :doh: )
Enfin, si je continue de "casser" le "chemin" de C à B comme je viens de le faire, à l'infinie, je me rapproche du segment [CB]... Qui lui fait (;)2) ! Pas 2 !
Je ne vois pas du tout où je me trompe... Est-ce qu'une âme charitable pourrait dans un élan de bonté que l'esprit des mathématiques lui insufflerait, m'aider à trouver mon erreur ? Merci infiniment !

PS : Ceci n'est pas un exercice de cours, c'est une énigme à laquelle j'ai fait face pendant que je faisais des maths pour mon plaisir personnel (j'aime beeeaaauuucoup les maths :3) donc pas besoin de tourner autour du pot pour me donner la réponse si vous ne voulez pas vous embêter à suivre le post en attendant que je trouve ^^ (Toutefois, si vous pouviez me mettre sur la voie plutôt que me dire tout de suite, je préférerais :3)

[fatal_error]

hello,

si tu prends à l'étape 2:
tu as, alignés : C,M',M,H',B
donc tous ces points appartiennent à [CB]
et CB = CM'+M'M+MH'+H'B
si tu calcules la distance de chacune de ces portions, ca doit etre genre 1/4 (t'as divisé CB par le nombre de portions)
et la longueur engendrée par les côté du triangle rectangle de la portion: sqrt(1/4/2)

du coup qqsoit le zoom que tu fais, la somme de tes deux ptits côtés sera tjs plus grande que ta portion de CB (d'où que t'obtiens pas sqrt(2) meme si visuellement on dirait).

par contre, si tu calcules l'aire couverte en ajoutant tes carrés, alors on peut espérer converger vers l'aire de ABC

[Ben314]

Salut,
Le problème, il est là :

...je me rapproche du segment [CB]...

Qu'est ce qui te fait croire (à tort) que lorsqu'un chemin est "proche" d'un autre leur longueur sont proches l'une de l'autre ?
Un tel résultat sera vrai (ou faux) en fonction de la définition que l'on prend du terme "proche".
Dans ton cas, les chemins sont "proches" dans le sens que tout point d'un des deux segment est proche d'un point de l'autre et cela n'est pas du tout suffisant comme définition pour en déduire que leur longueurs sont proches l'une de l'autre.

[Kakemo]

Bonjour ! Merci pour vos réponses, cependant, je ne vois toujours pas où je me suis trompé. :triste:

fatal_error > Je n'ai pas compris ton explication. En tout cas,

CB = CM'+M'M+MH'+H'B

C'est faux parce que C, M', M, M" et B sont alignés mais H appartient à [FM]... Il n'est pas aligné aux points énoncés précédemment, mais si tu penses quand même avoir raison, voudrais-tu bien m'expliquer autrement s'il te plaît , je n'ai pas bien compris désolé. ^///^

Ben314 > Euh, j'ai dit que je continuais de "couper" le chemin à l'infinie (un peu comme une fractale quoi). Du coup, la notion de limite entre en jeu parce que si on continue de "couper" (désolé je n'aime vraiment pas ce terme) le "chemin" (celui-là non plus ^^') à l'infinie, on obtient un segment allant de C à B... Donc [CB]... Gnaaaa ma tête fume ! :mur:

[Ben314]

Ben oui, mais que tu utilise le mot "limite" à la place des mots "proche de" ne change strictement rien à l'affaire donc je répète :
Qu'est ce qui te fait croire (à tort) que, lorsqu'une suite de chemins a pour limite un chemin donné, alors la longueur de ces chemins tend vers la longueur du chemin limite ?

L'exemple que tu donne montre tout simplement qu'une telle croyance est erronée, et que la notion de limite pour des chemins, (comme une bonne partie des maths, d'ailleurs) ça demande à être défini proprement pour pouvoir démontrer rigoureusement les propriétés que ça a (ou que ça n'a pas...)

[Kakemo]

Ben314 > D'aaaaccoooord j'ai compris ! :we:
Mais du coup où est-ce que je peux trouver des cours ou informations sur les limites concernant les "chemins" ?

[Ben314]

Je sais pas quel niveau tu as en math, mais en général, pour parler de "limite de chemins", on regarde les chemins comme des arcs paramétrés, c'est à dire des fonctions de [0,1]->R² (ou dans R^3 ou dans tout autre espace vectoriel normé).
L'ensemble des telles fonctions est alors un espace vectoriel (de dimension infini) que l'on peut munir de différentes topologies "classiques".
- La plus faible est celle dite de la "convergence simple" : pour qu'une suite fn converge vers f, on demande simplement que, pour tout t fixé, la suite fn(t) tende vers f(t). C'est une notion assez évidente, mais qui n'a a eu prés aucune "bonne" propriété : des chemins continus peuvent tout à fait tendre vers un chemin discontinu et, évidement, si une suite de chemin tend vers un chemin donné, ça ne prouve pas que leur longueur tende vers la longueur du chemin limite.
- Des tas d'autres topologies issues de normes "classiques" consistant par exemple à prendre comme distance entre deux chemins f et g le sup de ||f(t)-g(t)|| pour t entre 0 et 1 ou bien la racine de l'intégrale de 0 à 1 de ||f(t)-g(t)||² (qui a le bon gout d'être issue d'un produit scalaire) mais même pour ces distances "classiques", on peut toujours avoir des chemins qui tende vers un chemin donné sans que leur longueur ne tende vers la longueur du chemin limite.
- Si on veut qu'une telle propriété soit vraie, il faut que la distance utilisée "contrôle" les variations de f' de façon à ce que deux chemins "proches" (pour notre distance) aient des dérivées proches (et donc des longueurs proches).

[bolza]

Bonjour,

On peut noter :

le chemin BA-AC
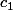le chemin CE-EM-MF-FB
....

Ensuite on peut définir la suite des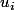 comme étant la longueur des chemins .
Donc :
= longueur du chemin
= longueur du chemin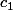
...

La suite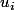 étant une suite constante égal à 2 elle converge (au sens de la convergence des suites)
vers 2 (qui est différent de racine 2).

Ce "paradoxe" est plus connue sous la forme énoncé sur cette page.

Pour mieux visualiser la chose, Imagine qu'à chaque étape, tu trace la droite parallèle à (BC) et reliant les "sommets" de ton chemin.

C'est-à-dire :
à l'étape 0 tu traces la droite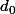 parallèle à (BC) et passant par A
à l'étape 1 tu traces la droite parallèle à (BC) et passant par E et F
à l'étape 2 tu traces la droite parallèle à (BC) et passant par E' F' G et H (pour reprendre tes notations).

Tu t'aperçoit que les droites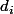 et (BC) "encadre" le chemin , pour tout i.
Tu t'aperçoit aussi que la distance entre les droites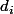 et (BC) converge vers 0.
Et donc en ce sens on peut dire que la suite des droite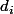 converge vers (BC).

On peut imaginer la suite des droites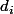 comme une seule droite en mouvement.
appelons la droite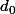 "d". Imagine que tu prend la droite d et que tu la pousse vers la droite (BC).
Ton chemin va se retrouver "écraser" de plus en plus entre les deux droites.

Mais aussi petit soit la distance entre d et (BC), tu pourra toujours tracer un chemin qui relie B et C d'une longueur
aussi grande que tu veux (et qui reste entre les deux droites), il suffit de faire "assez de zigzag".

Or quand tu "écrase" ton chemin, il ne "reste pas passif", il fait de plus en plus de "zigzag" pour que sa longueur reste constante.
Et c'est la le point délicat, qui est la cause du paradoxe, c'est que dans le cas limite où la droite d coïncide avec (BC),
ton chemin fait "une infinité de "zigzag" de longueur "infinitésimal" (pour pas dire 0).
Autrement dit quand la suite des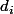 tend vers (BC) le nombre de "zigzag" tend vers l'infini.
En fait de manière plus formel à chaque étape, la longueur de ton chemin est où est le nombre de "zigzag".
Quand n tend vers l'infini, on a certes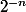 qui tend vers 0 (et donc visuellement cela se traduit par l'impression que l'on a que le chemin "s'applatit" sur (BC) )
Mais lui converge vers + infini, on obtient donc + infini * 0 qui est une forme indéterminée,
et un moyen de lever l'indétermination est de simplifié en 2, et donc la longueur limite du chemin est bien 2.

Bon je ne sais pas si tu arrives à visualiser ce que je veux dire ou si j'ai été clair,
mais j'espère que cela t'aura apporter quelques éléments de compréhension ^^