Bonjour,
Je rencontre des difficultés dans mon devoir maison de maths, pourriez-vous m'aider ?
J'ai une fonction définie sur I=]0;+infini[ telle que fn(x)= [(ln(x))^n] / x^2
ETUDE DE f1 (n=1)
1) Etudier les variations et les limites de f1
Ici j'ai dérivé la fonction et trouvé
f'(x) = (1-2ln(x)) / x^3
Raisonnant avec un tableau de signes et de variations, je trouve que f1(n) et croissante sur ]O;e^(1/2)[ et décroissante sur ]e^(1/2);+infini[
Et mes limites sont -infini en 0 et 0 en +infini
2) Prouver que pour tout entier naturel k>=2 : f1(k+1) ==2 par Sp= (ln2 /2^2) + (ln3 / 3^2) +...+ (lnp / p^2)
a: prouver que le suite (Sp) est croissante
b: par un processus de sommation, prouvez que :
Sp - (ln2 / 2^2) =< "intégrale de 2 à p" f1(t)dt =< Sp - (lnp / p^2)
4) Dériver la fonction suivante : f(x)= (1/X).(ln(x))
En déduire une méthode astucieuse pour calculer: "intégrale de 2 à p" (1/x^2)-(ln(x)/x^2)dx puis "intégrale de 2 à p"f1(t)dt
5) Déduire des questions précédentes que (Sp) est convergente
TS suites et intégrales
9 messages
- Page 1 sur 1
Salut !
2) Soit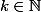 ,
,  ; comment varie
; comment varie  dans un intervalle de la forme
dans un intervalle de la forme 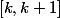 ?
?
Déduis-en que pour tout réel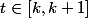 ,
, \le f(t) \le f(k)) , puis intègre sur ce même intervalle chaque membre de cette inégalité :+++:
, puis intègre sur ce même intervalle chaque membre de cette inégalité :+++:
3)a) Montre que .
.
b) Effectue la somme de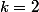 jusqu'à
jusqu'à 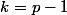 de chaque membre de l'inégalité obtenue dans la question 2) :
de chaque membre de l'inégalité obtenue dans la question 2) :
[CENTER]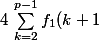 \le \sum_{k=2}^{p-1} \int_k^{k+1} f_1(t)\ {\rm d}t \le \sum_{k=2}^{p-1} f_1(k)) [/CENTER]
[/CENTER]
2) Soit
Déduis-en que pour tout réel
3)a) Montre que
b) Effectue la somme de
[CENTER]
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:3)a) Montre que.
Pour montrer ca, exprime juste
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
6154433426 a écrit:Puis-je dire que Sp+1 = Sp + [(lnp+1)/(p+1)^2] ?
Oui, c'est ça ; après en justifiant que [(lnp+1)/(p+1)^2]>0, tu obtiens Sp+1 - Sp > 0 :++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
6154433426 a écrit:D'accord merci !
Comment déduire que Sp est convergente ?
Et pour la 4° question, j'ai dérivé et trouvé f'(x)=(1/x^2) - xln(x) sauf que je ne trouve pas de "méthode astucieuse"
(S_p) est une suite croissante, quelle condition manque-t-il pour affirmé qu'elle converge ?
Ta dérivée n'est pas bonne : la réponse t'es donnée dans la question : normalement, tu dois trouver
Pour le calcul, remarque ensuite que si
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
