Aide
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdiphone
- Membre Naturel
- Messages: 46
- Enregistré le: 31 Oct 2014, 16:30
-
 par mehdiphone » 17 Jan 2015, 18:27
par mehdiphone » 17 Jan 2015, 18:27
comme je l'ai dit je commence ce chapitre et j'aimerai être familiarisé avec certains type d'exos ..
soit
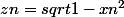
montrer que
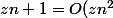)
quelqu'un peut m'aider à le faire merci
-
mehdiphone
- Membre Naturel
- Messages: 46
- Enregistré le: 31 Oct 2014, 16:30
-
 par mehdiphone » 17 Jan 2015, 19:10
par mehdiphone » 17 Jan 2015, 19:10
mehdiphone a écrit:comme je l'ai dit je commence ce chapitre et j'aimerai être familiarisé avec certains type d'exos ..
soit
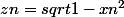
montrer que
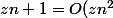)
quelqu'un peut m'aider à le faire merci
quelqu'un?
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 17 Jan 2015, 19:25
par Pythales » 17 Jan 2015, 19:25
mehdiphone a écrit:comme je l'ai dit je commence ce chapitre et j'aimerai être familiarisé avec certains type d'exos ..
soit
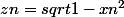
montrer que
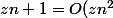)
quelqu'un peut m'aider à le faire merci
Qu'est ce que c'est que

? C'est
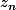
(indice) ou

?
et

? c'est
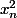
ou

?
et

? c'est
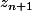
ou

ou

?
-
mehdiphone
- Membre Naturel
- Messages: 46
- Enregistré le: 31 Oct 2014, 16:30
-
 par mehdiphone » 17 Jan 2015, 19:26
par mehdiphone » 17 Jan 2015, 19:26
Pythales a écrit:Qu'est ce que c'est que

? C'est
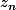
(indice) ou

?
et

? c'est
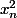
ou

?
et

? c'est
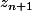
ou

ou

?
c'est
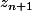
et c'est
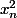
excusez moi j'ai un peu de mal.. merci
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 17 Jan 2015, 20:10
par Pythales » 17 Jan 2015, 20:10
mehdiphone a écrit:c'est
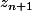
et c'est
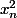
excusez moi j'ai un peu de mal.. merci
Quelle est la relation de récurrence sur les

?
-
mehdiphone
- Membre Naturel
- Messages: 46
- Enregistré le: 31 Oct 2014, 16:30
-
 par mehdiphone » 17 Jan 2015, 20:16
par mehdiphone » 17 Jan 2015, 20:16
Pythales a écrit:Quelle est la relation de récurrence sur les

?
mince j'avais pas fait attention,

appartient ]0;1[

=(

) /(1+

} MONTRER que

appartient [0;1] et s'en suit la question de départ !
-
mehdiphone
- Membre Naturel
- Messages: 46
- Enregistré le: 31 Oct 2014, 16:30
-
 par mehdiphone » 17 Jan 2015, 21:08
par mehdiphone » 17 Jan 2015, 21:08
mehdiphone a écrit:mince j'avais pas fait attention,

appartient ]0;1[

=(

) /(1+

} MONTRER que

appartient [0;1] et s'en suit la question de départ !
quelqu'un peut m'aider à le faire je ne comprend rien!

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 17 Jan 2015, 21:19
par zygomatique » 17 Jan 2015, 21:19
mehdiphone a écrit:quelqu'un peut m'aider à le faire je ne comprend rien!
salut
tu veux qu'on t'aide ? ....
alors donne-nous un énoncé complet et sans erreur ....
:mur:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
mehdiphone
- Membre Naturel
- Messages: 46
- Enregistré le: 31 Oct 2014, 16:30
-
 par mehdiphone » 17 Jan 2015, 21:33
par mehdiphone » 17 Jan 2015, 21:33

appartient ]0;1[

=(

) /(1+

) MONTRER que

appartient [0;1]
soit
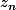
=

montrer que
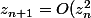)
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 17 Jan 2015, 21:43
par Pythales » 17 Jan 2015, 21:43
mehdiphone a écrit:mince j'avais pas fait attention,

appartient ]0;1[

=(

) /(1+

} MONTRER que

appartient [0;1] et s'en suit la question de départ !
En étudiant la fonction

tu démontres par récurrence que

Tu établis ensuite que
^2})
soit ...
-
mehdiphone
- Membre Naturel
- Messages: 46
- Enregistré le: 31 Oct 2014, 16:30
-
 par mehdiphone » 18 Jan 2015, 13:14
par mehdiphone » 18 Jan 2015, 13:14
Pythales a écrit:En étudiant la fonction

tu démontres par récurrence que

Tu établis ensuite que
^2})
soit ...
bien vu! merci pour la 1 en étudiant la fonction on remarque que la fonction est croissante de 0 jusqu'à 1 et décroissante vers 0 donc avec une récurrence j'ai réussi à démontré cela maintenant la 2e partie me pose problème. pouvez vous détailler en m'expliquant l'aide que vous m'avez apporté?
-
mehdiphone
- Membre Naturel
- Messages: 46
- Enregistré le: 31 Oct 2014, 16:30
-
 par mehdiphone » 18 Jan 2015, 13:38
par mehdiphone » 18 Jan 2015, 13:38
mehdiphone a écrit:bien vu! merci pour la 1 en étudiant la fonction on remarque que la fonction est croissante de 0 jusqu'à 1 et décroissante vers 0 donc avec une récurrence j'ai réussi à démontré cela maintenant la 2e partie me pose problème. pouvez vous détailler en m'expliquant l'aide que vous m'avez apporté?
quelqu'un?
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 18 Jan 2015, 16:26
par Pythales » 18 Jan 2015, 16:26
mehdiphone a écrit:bien vu! merci pour la 1 en étudiant la fonction on remarque que la fonction est croissante de 0 jusqu'à 1 et décroissante vers 0 donc avec une récurrence j'ai réussi à démontré cela maintenant la 2e partie me pose problème. pouvez vous détailler en m'expliquant l'aide que vous m'avez apporté?
^2}}=...)
continue
-
mehdiphone
- Membre Naturel
- Messages: 46
- Enregistré le: 31 Oct 2014, 16:30
-
 par mehdiphone » 18 Jan 2015, 20:24
par mehdiphone » 18 Jan 2015, 20:24
Pythales a écrit:^2}}=...)
continue
=
-4x_n/((1+x_n)^2)})
pour obtenir le "o(zn^2) je doit faire un DL nan ?
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 18 Jan 2015, 23:20
par Pythales » 18 Jan 2015, 23:20
mehdiphone a écrit:=
-4x_n/((1+x_n)^2)})
pour obtenir le "o(zn^2) je doit faire un DL nan ?
Je t'ai déjà donné la réponse.
(Refais ton calcul. Il est faux)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
tu démontres par récurrence que

^2})