Théorème des Accroissements Finis =)

[_-Gaara-_]

Salut à tous =)

Je voudrais vous demander si vous auriez des exercices intéressants sur les Accroissements finis afin de m'y habituer. J'ai lu ce qu'il y avait sur wikipédia mais je ne vois vraiment pas comment l'appliquer dans un exercice.

Voilà Merci =)

[J-R]

bonjour

si c'est le commencement je peut t'en proposer un facile sur les inégalités des accroissement finis:

Montrer que :

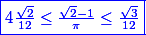
j'en ai des autres ...

[_-Gaara-_]

D'accord =)

je m'y met tout de suite


Merci :D

[_-Gaara-_]

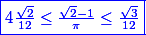
Humm, je ne sais même pas par quoi commencer >.<

j'ai essayé d'élever au carré ce qui donne :



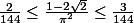
Je ne vois pas comment procéder =(

[J-R]

et si je te parlais de fonction sinus...

essaie de trouver un intervalle qui pourrait correspondre

[Joker62]

Tu demandes un exo sur le TAF
Donc pense quand même a essayer d'appliquer le théorème lol

[_-Gaara-_]

humm ^^

voilà ce que je trouve :




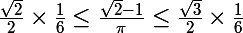
donc

[_-Gaara-_]

Tu demandes un exo sur le TAF
Donc pense quand même a essayer d'appliquer le théorème lol

lol ouai mais je ne vois pas comment l'appliquer

[Joker62]

Trouves toi une fonction, un intervalle et réfléchi à ce que dit le théorème.
Bon sauf qu'ici ça sera l'inégalité des accroissements finis, mais c'est pareil ! :)

[_-Gaara-_]

:cry: Zut alors, je ne trouves pas de fonction =( chui nul :briques:

j'ai beau lire et relire wikipédia je ne vois pas comment l'appliquer ici >.<

il n'y a pas de x ou de a ou de b XD :briques:

[J-R]

Zut alors, je ne trouves pas de fonction =( chui nul

j'ai beau lire et relire wikipédia je ne vois pas comment l'appliquer ici >.<

il n'y a pas de x ou de a ou de b XD

lol

mais non je trouve que c'est bien de s'intéresser à des notions comme ca pour ne pas rester dans le terre à terre...

ca vient pas comme ca surtout si c'est le premier.

considère la fonction sinus sur l'intervalle

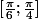
maintenant il est tué l'exo car le but principal est de recherché cette fonction et l'intervalle.

enfin comme ca tu verras une application

[Joker62]

Et comment on fait pour la rechercher cette fonction ?

Alors on reprend l'inégalité en question du théroème :

Soit f : [ab] -> R
si f continue sur [ab] dérivable sur ]ab[ alors s'il existe M € R tel que
|f'(x)| < M pour tout x € ]ab[

On a :
|f(b)-f(a)| <= M.|b-a|


On va le faire avec l'inégalité de droite :





Et donc là, suffit de vérifier que sin(pi/4) = Racine(2)/2
Racine(pi/6) = 1/2

Et conclure

[_-Gaara-_]

J'essaye de chercher pour l'autre =)

donc on a :



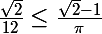
donc



donc



donc



et c'est bon ? :id: :id:


et donc sachant que pi/12 appartients à [pi/6;pi/4] ce résultat est vrai d'après l'inégalité des accroissements finiiiiiiiiiiiiiiiiiiiiiiis :zen:

c'est juste ??

[J-R]

je ne comprend pas ta méthode pour raisonner.

si on part de ce que lon sait, logiquement on devrait poursuivre par équivalence.

aussi joker je n'ai pas compris comment tu faisais pour choisir ta fopnction mais bon ... on a pas le meme intervalle.

je propose ma solution:

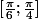
soit la fonction f définie sur par .

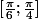
f est dérivable sur et .

f' est décrsoissante sur et bornée par les réels et .

on a donc sur :



donc là on appliqie le TAF et on obtient:



d'où

cqfd

c'est trop beau l'analyse. vivement l'an prochain

@+

[_-Gaara-_]

Absolument génial !!


Dis J-R tu en as une autre ? je vais essayer de bien la rédiger =)

Merciiiiii :we:

[J-R]

si si je comprend mieux ton raisonnement mais il aurait été plus rigoureux de raisonner par équivalence.

sinon je reste perplexe sur:

donc sachant que pi/12 appartients à [pi/6;pi/4]

...

[Joker62]

J'avais la même fonction que toi JR, sauf que j'ai pas poursuivi...

Sinus sur Pi/6 ; Pi/4

[J-R]

ok j'ai un autre exo qui permet de démontrer la divergence de la série harmonique:

démontrer que:



en déduire que la série harmonique diverge vers

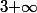
[_-Gaara-_]

si si je comprend mieux ton raisonnement mais il aurait été plus rigoureux de raisonner par équivalence.

sinon je reste perplexe sur: ...

looooool :ptdr:

je dis nawak !! :briques:

[_-Gaara-_]

^^ dans ce cas c'est plus dur de trouver l'intervalle

bon j'essaye et je te dis ce que je trouve =)