Théorème des Accroissements Finis =)

[Nightmare]

Salut :happy3:

Un exo sympas sur le TAF :

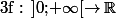
On considère dérivable et telle que f' converge vers l en +oo.

Montrer que converge aussi vers l en +oo.

(Le résuitat est-il vrai si f' tend vers l'infini?)

[_-Gaara-_]

Saluut Nightmare ^^


je vais tenter de le faire =)

[_-Gaara-_]

Bon voilà j'arrive à çà :

f(x) sur ]0;x[ avec x>0

f dérivable sur ce même intervalle ]0;x[ (+ continue sur [0;x] ? )

On applique le TAF et on trouve



Mais après je ne sais pas quoi faire :triste: :triste:

[Nightmare]

C'est un peu plus difficile que ce que tu as fait avant, ce n'est pas une application directe du TAF, il faut réfléchir un peu plus :lol3:

[_-Gaara-_]

Oki =)

Mais est-ce que j'aurais besoin de la définition fonctionnelle de la limite ? C'est à dire avec les epsilon et tout ? :id:

[Nightmare]

C'est possible :happy3:

[raito123]

C'est possible :happy3:

Vas y un petit indice ! c'est la premiére fois que je vois un truc pareil !!

[Nightmare]

Un petit indice? Utiliser le TAF :lol2:

Un indice plus gros : On a envie de rattacher f(x)/x à f'. L'idée est évidemment d'utiliser le TAF. Sauf qu'on voit que ça marche pas vraiment en 0.

Par contre, on sait que f' converge. L'idée est donc qu'après un certain A, |f'(x)-l|<epsilon
Regarder ce qu'il se passe du côté de

:happy3:

[raito123]

Alala l'idée est là mais impossible de la faire sortir aye aye aye !!!!

Si on fait tendre A en +oo alors sera presque f'(A) !!!


Je sais ça n'as pas de sens GRrrrrrr!!!

[raito123]

Ok je tente quuelque chose :

on a f continu sur [A,x] et dérivable sur ]A,x[ donc d'aprés TAF :



On a

Donc

Là on peut rien faire "piste fermée" car f ne continu pas en 0 !!!!!!

[fati]

salut tout le monde! j'ai trouvé la réponse! enfin je pense :s!
Indice on revient à la définition de la limite! et puis TAF

[raito123]

T'avais dis que tu allais poster la réponse pk t'as changer ??

t'as pas tout trouver?

[Nightmare]

Il y a une méthode qui n'utilise pas le TAF et qui est rapide mais bon ce n'est pas le sujet du topic :lol3:

[raito123]

Il y a une méthode qui n'utilise pas le TAF et qui est rapide mais bon ce n'est pas le sujet du topic :lol3:

Vas y ça sera util !!!

[fati]

non j'ai trouvé! mais je sais pas utiliser le latex et la méthode que j'ai utilisé a vraiment besoin de latex!

[Nightmare]

Deuxième méthode :

D'après l'énoncé on a au voisinage de +oo
L'application constante 1 n'est pas intégrable sur [a;+oo[ d'où :

ie :

Par conséquent :

D'où :
CQFD

:happy3:

[raito123]

J'ai saisit cette méthode merci nightmare!!


Tu peux voir auprés de celle du post n°70 pasque la 1ére méthode j'arrive pas à trouver le bon résultas!!??

[Nightmare]

Tu es bien lancé.

Essaye de trouver une relation entre f(x)/x et (f(x)-f(A))/(x-a)

:happy3:

[raito123]

Si on avait quelque information sur f on pourrait faire |f(x)/x|>|[f(x)-f(A)]/x-A| ou le l'inverse...


Là on peut rien faire. Plutôt je ne vois pas comment faire !!?

[Nightmare]

Je voulais plutot dire, essaye d'exprimer f(x)/x en fonction de (f(x)-f(A))/(x-A)