Théorème des Accroissements Finis =)
alors si on prend une fonction f continue sur un intervalle I et qui est strictement monotone sur I alors on dit que cette fonction réalise une bijection de I dans I.
en d'autre termes, pour tout réel appartenant à f(I) (qui est un intervalle par la strcite monotonie de f) il existe un unique antécédent appartenant à I par f.
(on peut aussi définir la notion de bijectivité avec les application injective et surjective (une fonction est bijective si elle est à la fois injective et surjective)).
par conséquent on peut définir la fonction g qui à tout réel de f(I) associe un unique réel de I.
g est appelé bijection réciproque. et on note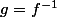
on a : f(x)=y x=g(y).
on déduit facilement que gof=id.
exemple: la bijection réciproque de la fonction exponentielle est la fonction logarithme népérien.
pour tout réel x, exp(x)=y x=ln(y) .
aussi f une bijection dérivable de I sur J.
soit a un réel de I tel que\neq 0.)
alors la fonction est dérivable en f(a) et :
est dérivable en f(a) et : =\frac{1}{f'of^{-1}(a)})
je t'invite à consulter les cours sur le site où tu es nouvelment inscris depuis hier
en d'autre termes, pour tout réel appartenant à f(I) (qui est un intervalle par la strcite monotonie de f) il existe un unique antécédent appartenant à I par f.
(on peut aussi définir la notion de bijectivité avec les application injective et surjective (une fonction est bijective si elle est à la fois injective et surjective)).
par conséquent on peut définir la fonction g qui à tout réel de f(I) associe un unique réel de I.
g est appelé bijection réciproque. et on note
on a : f(x)=y x=g(y).
on déduit facilement que gof=id.
exemple: la bijection réciproque de la fonction exponentielle est la fonction logarithme népérien.
pour tout réel x, exp(x)=y x=ln(y) .
aussi f une bijection dérivable de I sur J.
soit a un réel de I tel que
alors la fonction
je t'invite à consulter les cours sur le site où tu es nouvelment inscris depuis hier
Merciiiiiii J-R ! J'ai compris  héhéhé
héhéhé
juste une précision ^^ id = constante ??
J'ai trouvé çà concernant l'arctan :
http://fr.wikipedia.org/wiki/Fonction_arctangente
et je vais regarder sur le site hihi
c'est sous quelle rubrique ? Lycée ? ou Prépa ? =)
Encore merciiii
Je continue à chercher je ne laisserai pas tomber !! =)
juste une précision ^^ id = constante ??
J'ai trouvé çà concernant l'arctan :
http://fr.wikipedia.org/wiki/Fonction_arctangente
et je vais regarder sur le site hihi
c'est sous quelle rubrique ? Lycée ? ou Prépa ? =)
Encore merciiii
Je continue à chercher je ne laisserai pas tomber !! =)
lol :we:
id est la fonction identité, f: x ---> x. (tous les points sont fixes).
sinon tu vas dans : lycée --> terminale ---> cours et exercices ---> continuité-dérivabilité et tu as un superbe doc
le wiki sa devient complètement hors programme (je ne me suis pas encore intéréssé aux séries) mais sinon ca résume ce que je t'ai dit pour la fonction angente.
juste une précision ^^ id = constante
id est la fonction identité, f: x ---> x. (tous les points sont fixes).
sinon tu vas dans : lycée --> terminale ---> cours et exercices ---> continuité-dérivabilité et tu as un superbe doc
le wiki sa devient complètement hors programme (je ne me suis pas encore intéréssé aux séries) mais sinon ca résume ce que je t'ai dit pour la fonction angente.
voilààà
http://pagesperso-orange.fr/gilles.costantini/Lycee_fichiers/CoursT_fichiers/deriv03.pdf
c'est bien ce doc là ? Il y a en plus un truc sur l'étude de la fonction tangeante !! çà à l'air intéressant =)
Merci
Je me remets donc tout de suite à la démonstration =)
http://pagesperso-orange.fr/gilles.costantini/Lycee_fichiers/CoursT_fichiers/deriv03.pdf
c'est bien ce doc là ? Il y a en plus un truc sur l'étude de la fonction tangeante !! çà à l'air intéressant =)
Merci
Je me remets donc tout de suite à la démonstration =)
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 93 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
