Théorème des Accroissements Finis =)

[fati]

f( x)/x= ((f (x ) - f (A))/x-a)*(1-A/x) + f(A)/x
c'est juste?

[raito123]

f( x)/x= ((f (x ) - f (A))/x-a)*(1-A/x) + f(A)/x
c'est juste?

Ouais donc

[Nightmare]

C'est bon fati :happy3:

C'est presque terminé!

Je vais me coucher je vous en laisse un autre pour les insomniaques :

Soit f dérivable sur R convexe et telle que

Montrer que

Bon courage

:happy3:

[raito123]

C'est bon fati :happy3:

C'est presque terminé!

Je vais me coucher je vous en laisse un autre pour les insomniaques :

Soit f dérivable sur R convexe et telle que

Montrer que

Bon courage

:happy3:

Atta stp



ça veut dire quoi?

[Nightmare]

Regarde sur wiki "équivalent" et "convexe" ça m'évitera de tout expliquer :lol:

[fati]

convexe= mou7adab! concave= mou9a3ar!

[J-R]

salut nightmare et fati

je me colle à l'exo de nightmare:

f' converge vers l

[TEX]3$\forall r\in \mathbb{R}^{+*},\exists a\in \mathbb{R}^{+*}/x>a => l-ra, (x-a)(l-r)[TEX] 3$x>a, (x-a)(l-r)+f(a) [TEX]3$x>a, \frac{(x-a)(l-r)+f(a)}{x}0

ca doit converger vers l normalement...

edit: erreur entre a et x...

[raito123]

Bonjours, J-R

Et comment prouver que ça converge vers l ?

[Nightmare]

Salut :happy3:

ca doit converger vers l normalement...

Il y a juste un problème pour une certaine valeur d'une certaine variable. Laquelle?

[J-R]

benh euh... j'ai deja eu du mal à dire que ca convergeait vers l (faudrait faire une bidouille mais bon...)

on a
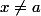
sinon je propose r=l (a priori c'est valable pour tout réel positf r...).

[Nightmare]

effectivement pour r=l il y a un problème.

Bref pour s'en débarrasser on utilise la relation qu'a trouvée Fati :



On a alors :

ie :


Or converge vers 0 donc est inférieur à epsilon à partir d'un certain rang b > a
Et donc lorsque x > a, d'où f(x)/x converge vers l (pour faire propre on aurait dû prendre epsilon/2 au début)

:happy3:

[raito123]

Je reprend ce que j'ai commencer :

donc

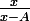
Au voisinage de +oo tend vers 0 et tend vers 1 donc ce qui reste

Alors c'est bon??

[Nightmare]

Tu ne peux pas vraiment passer à la limite comme cela, bien qu 'intuitivement c'est ce qu'on veut faire, il faut le justifier en repassant à la définition avec les quantificateurs.

[raito123]

Ok je viens de voir ton post et j'ai tout compris !!!!

Merci!!

En fait j'ai une question à propos de ta 2éme méthode !!

Deuxième méthode :

D'après l'énoncé on a au voisinage de +oo
L'application constante 1 n'est pas intégrable sur [a;+oo[ d'où :

:happy3:

Est-ce une définition : ?

Et ça veut dire quoi exactement ??

Merci

[Nightmare]

tu n'as pas vu les petits o ?

En gros si on prend deux fonctions f et g, on dit que f=o(g) au voisinage de a (qui se lit : f est un petit o de g) lorsqu'il existe une fonction h qui converge vers 0 en a telle que f(x)=h(x)g(x).
Ou simplement si g ne s'annule pas au voisinage de a, f=o(g) si et ssi f/g converge vers 0 en a.

D'après toi alors, qu'est-ce qu'un o(1) ?

[raito123]

Je pense que les petits o sont au programmes du sup c'est ça?

Par exemple : f(x)=o(1) au voisinage d'un certain a alors la limite de f en a est égale à 0 c'est ça ??


O se prononce comme la lettre "o" ou "ron" ou quoi?

[Nightmare]

oui voila, o(1) est une fonction qui converge vers 0.

o se lit comme la lettre. L'étude des petits o est effectivement au programme de sup.

[raito123]

Ok nightmare merci j'ai compris les deux demo à merveille!!

En ce qui concerne l'equivalence c'est le comportement d'une fonction par rapport à une autre c'est ça ??

Tu peux me donner un exo facile pour commencer ???

[Nightmare]

On gros deux fonctions équivalents se "comportent" de la même manière au voisinage en question.

Tu veux des exos sur quoi? les équivalents ou le TAF?

[raito123]

TAF je sais m'en servir !!!


Les equivalences c'est nouveau pour moi donc si c'est possible un peu de tout !!