Est-ce que quelqu'un pourrait m'aider pour répondre à cette question:
Soit la suite (In) définie pour tout entier n par: In = intégrale de 1 à e de x(lnx)^n dx.
Question: démontrer que l=0.
Merci d'avance.
Suites d'intégrales
10 messages
- Page 1 sur 1
Re: Suites d'intégrales
bonsoir,
1° fais le changement de variable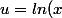)
2° majore et minore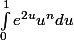 par deux suites de limite nulle
par deux suites de limite nulle
1° fais le changement de variable
2° majore et minore
Re: Suites d'intégrales
ce qui permet d'encadrer In entre deux intégrales qui tendent vers zéro quand n tend vers l'infini
Re: Suites d'intégrales
D'accord j'ai compris mais pourquoi lors de la deuxième étape, on a e^2u u^n car si on change la variable, ça fait x(u)^n.
Merci.
Merci.
Re: Suites d'intégrales
ce qu'il faut retenir:
une fonction continue sur un intervalle compact [a;b] est bornée et atteint ses bornes.
par exemple sur [0;1]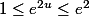
une fonction continue sur un intervalle compact [a;b] est bornée et atteint ses bornes.
par exemple sur [0;1]
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 101 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
