Propriété de sigma ?
26 messages
- Page 1 sur 2 - 1, 2
propriété de sigma ?
Bonjour
J'aimerais savoir si on pouvait écrire : sigma(xi*f(xi))=x*sigma(f(xi))
Ou s'il existerait des fonctions particulières pour lesquelles l'égalité est vraie.
Merci, et désolé pour la notation, j'ai oublié comment faire des beaux sigma majuscule.
J'aimerais savoir si on pouvait écrire : sigma(xi*f(xi))=x*sigma(f(xi))
Ou s'il existerait des fonctions particulières pour lesquelles l'égalité est vraie.
Merci, et désolé pour la notation, j'ai oublié comment faire des beaux sigma majuscule.
Re: propriété de sigma ?
salut
comme appris au collège pour toute somme de produits on ne peux factoriser que par un facteur commun ....
comme appris au collège pour toute somme de produits on ne peux factoriser que par un facteur commun ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: propriété de sigma ?
Oui, mais qui te dit que la somme en question c'est pas ) (qui est égale à
(qui est égale à ) , voire même à
, voire même à ) ...)
...)
P.S. Joke...
P.S. Joke...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: propriété de sigma ?
Arrêtez donc de vous moquer et regardez plutôt (entretemps j'ai rappris à me servir de l'éditeur d'équations).
J'ai obtenu dans une démonstration l'égalité=(n+1)*f_n(x))
D'où}=\sum_{i=0}^{x}{(n+1)*f_n(x_i)})
Or ma fonction est définie telle que
est définie telle que =\sum_{i=0}^{x}{f_n(x_i)})
Donc*f_n(x_i)}=(n+1)*f_n_+_1(x))
Enfin}=(n+1)*f_n+_1(x_i)})
Donc avec mon égalité de départ, j'obtiens}=x*f_n(x+1))
J'ai obtenu dans une démonstration l'égalité
D'où
Or ma fonction
Donc
Enfin
Donc avec mon égalité de départ, j'obtiens
Modifié en dernier par lulu math discovering le 09 Fév 2016, 17:34, modifié 3 fois.
Re: propriété de sigma ?
Avant de regarder ta prose, je te rapelle que, dans le post de départ (donc le seul qu'on avait à notre disposition) :
1) On ne savait pas quelles étaient les fonctions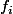 , ni même les ensemble de départ et d'arrivé des fonctions en questions (réels ? complexes ? vecteur ?)
, ni même les ensemble de départ et d'arrivé des fonctions en questions (réels ? complexes ? vecteur ?)
2) Pas plus d'info. concernant les , ni même leur nature.
, ni même leur nature.
3) Pas d'info non plus relative à la somme en question (somme finie ? infinie ? sur quels indices ? de combien à combien ?)
4) Aucune info non plus concernant un éventuel lien entre le de ta formule et le reste des données.
de ta formule et le reste des données.
Ma première idée de réponse à clairement été de te répondre "Bien sûr qu'on peut, il suffit de poser}}{\sum{x_i}}) modulo de supposer
modulo de supposer 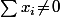 "
"
Bref, il faudrait éventuellement comprendre qu'on a peut être un certain bagage en mathématique, mais... qu'on a pas de boule de cristal...
Donc, effectivement, à part faire de l'humour, je vois vraiment pas ce qu'on aurait pu faire d'autre avec ce "rien" comme énoncé.
Et là, c'est "guère mieux" : par exemple, si effectivement=xf_n(x)) vu que tu somme en i un truc qui dépend pas de i.
vu que tu somme en i un truc qui dépend pas de i.
1) On ne savait pas quelles étaient les fonctions
2) Pas plus d'info. concernant les
3) Pas d'info non plus relative à la somme en question (somme finie ? infinie ? sur quels indices ? de combien à combien ?)
4) Aucune info non plus concernant un éventuel lien entre le
Ma première idée de réponse à clairement été de te répondre "Bien sûr qu'on peut, il suffit de poser
Bref, il faudrait éventuellement comprendre qu'on a peut être un certain bagage en mathématique, mais... qu'on a pas de boule de cristal...
Donc, effectivement, à part faire de l'humour, je vois vraiment pas ce qu'on aurait pu faire d'autre avec ce "rien" comme énoncé.
Et là, c'est "guère mieux" : par exemple, si effectivement
Alorslulu math discovering a écrit:
Modifié en dernier par Ben314 le 09 Fév 2016, 15:53, modifié 4 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: propriété de sigma ?
ce qui équivaut à }=x*\sum_{i=0}^{x}{f_n-_1(x_i+1)})
Modifié en dernier par lulu math discovering le 09 Fév 2016, 15:57, modifié 1 fois.
Re: propriété de sigma ?
Désolé je viens de voir ton message.
Je comprends ton point de vue, j'aurais dû vous donner des infos supplémentaires, mais je voulais déjà savoir si l'égalité était évidente, ou si il y avait des cas précis où elle s'appliquait.
Et puis, sans l'éditeur TEX, expliquer clairement la situation me semblait hautement improbable
Enfin, bon courage pour ma prose.
Je comprends ton point de vue, j'aurais dû vous donner des infos supplémentaires, mais je voulais déjà savoir si l'égalité était évidente, ou si il y avait des cas précis où elle s'appliquait.
Et puis, sans l'éditeur TEX, expliquer clairement la situation me semblait hautement improbable
Enfin, bon courage pour ma prose.
Re: propriété de sigma ?
Éditeur ou pas éditeur, je pense pas que ça résolve franchement le problème.
Là, on devine que est un entier naturel (éventuellement nul ? ça on sait pas...)
est un entier naturel (éventuellement nul ? ça on sait pas...)
Au début, on devine que est un réel et puis tout d'un coup non, il faut (re)deviner que c'est un entier (vu qu'il apparait en haut d'un symbole sigma), encore qu'on se demande si c'est bien un entier où pas une notation un peu bizarre vu que de noter
est un réel et puis tout d'un coup non, il faut (re)deviner que c'est un entier (vu qu'il apparait en haut d'un symbole sigma), encore qu'on se demande si c'est bien un entier où pas une notation un peu bizarre vu que de noter  un entier, c'est pas classique.
un entier, c'est pas classique.
Tu crois pas que ça serait légèrement plus simple de préciser à quoi correspondent les symboles (=lettres) que tu utilise avant de les utiliser ?
Là, on devine que
Au début, on devine que
Tu crois pas que ça serait légèrement plus simple de préciser à quoi correspondent les symboles (=lettres) que tu utilise avant de les utiliser ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: propriété de sigma ?
lulu math discovering a écrit:Je pense que c'est bon là.
Alors qu'en penses-tu ?
1) Est-ce que
2) Les fonctions
3)
Modifié en dernier par Ben314 le 09 Fév 2016, 16:07, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: propriété de sigma ?
Décidément, j'ai vraiment fait n'importe quoi.
n est un entier positif (une variable)
x est un entier positif (une variable)
Les deux peuvent être nuls. Encore que si tu veux on peut les considérer non-nuls, c'est pas gênant dans ma démonstration.
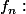 |N ->|N
|N ->|N
n est un entier positif (une variable)
x est un entier positif (une variable)
Les deux peuvent être nuls. Encore que si tu veux on peut les considérer non-nuls, c'est pas gênant dans ma démonstration.
Re: propriété de sigma ?
4) C'est quoi les  ? des réels fixés au départ qui sont les même du début à la fin de ta prose ?
? des réels fixés au départ qui sont les même du début à la fin de ta prose ?
5) ça :
Et si c'est effectivement une formule de récurrence, ben ça manque cruellement d'amorce(=initialisation) : que vaut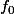 ?
?
5) ça :
ça ressemble vaguement à une formule de récurrence, sauf qu'on sait pas si c'est le cas où pas vu qu'il n'est pas précisé si cette formule est valable "pour tout n" ou bien pour un n particulier ni si elle est valable "pour tout x" ou pour un x particulier.lulu math discovering a écrit:Or mes fonctionssont définies telles que
.
Et si c'est effectivement une formule de récurrence, ben ça manque cruellement d'amorce(=initialisation) : que vaut
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: propriété de sigma ?
La fonction (si tu préfères)  est définie pour tous entiers positifs x et n telle que :
est définie pour tous entiers positifs x et n telle que :
=x)
=\sum_{i=0}^{x}{f_n(x_i)})
Re: propriété de sigma ?
Je suppose que c'est :
et que_{i\in{\mathbb N}) est une suite d'entiers fixés une bonne fois pour toute.
est une suite d'entiers fixés une bonne fois pour toute.
Sinon, pour mettre plus d'un caractère en indice (ou exposant), il faut mettre f_{n+1} avec des accolades.
lulu math discovering a écrit:
et que
Sinon, pour mettre plus d'un caractère en indice (ou exposant), il faut mettre f_{n+1} avec des accolades.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: propriété de sigma ?
Si effectivement c'est bien ça alors déjà, ça :  et tout
et tout  on a ...").
on a ...").
Pour on a
on a =x(x\!+\!1)) alors que
alors que  f_n(x)=(n\!+\!1)\sum_{i=0}^x x_i) et je ne vois aucun rapport entre les deux.
et je ne vois aucun rapport entre les deux.
C'est faux (modulo comme d'hab. d'interpréter la formule comme disant "pour toutlulu math discovering a écrit:J'ai obtenu dans une démonstration l'égalité
Pour
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: propriété de sigma ?
Merci pour l'astuce.
Concernant la suite d'entiers) , j'ai encore écrit n'importe quoi !!!
, j'ai encore écrit n'importe quoi !!! 

C'est=\sum_{i=0}^{x}{f_n(i)})
à chaque fois que j'ai écris , c'était i !!!!
, c'était i !!!!
Concernant la suite d'entiers
C'est
à chaque fois que j'ai écris
Re: propriété de sigma ?
A force de regarder dans tout les sens ton post., je suis en train de me demander si, ce que tu cherche à calculer, ça ne serait pas par hasard =0^n+1^n+2^n+\cdots+x^n) avec
avec 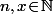
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: propriété de sigma ?
Non, mais c'est du même type. D'autant plus que je ne cherche pas à calculer, mais à démontrer l'expression de )
En l'occurrence=\prod_{i=0}^{n}{(x+i)/(i+1)})
sachant que f_n est définie telle que (pour bien l'écrire)
=x)
=\sum_{i=0}^{x}{f_n(i)})
évidemment pour tous entiers positifs x et n
Ce serait assez dur à expliquer je pense, techniquement) serait une "somme cumulée" des entiers de 0 à x
serait une "somme cumulée" des entiers de 0 à x
Je vais réécrire toute ma prose pour qu'elle devienne intelligible.
En l'occurrence
sachant que f_n est définie telle que (pour bien l'écrire)
évidemment pour tous entiers positifs x et n
Ce serait assez dur à expliquer je pense, techniquement
Je vais réécrire toute ma prose pour qu'elle devienne intelligible.
Re: propriété de sigma ?
Bon, ben on va repartir de zéro, je pense que ça ira plus vite :
On considère la fonction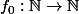 définie par :
définie par : =x) .
.
Puis, pour tout dans
dans 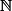 , on définie par récurrence la fonction
, on définie par récurrence la fonction 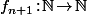 par :
par : \!=\!\sum_{i=0}^xf_n(i)) .
.
Dans ce cas, on a\!=\!\dfrac{x(x\!+\!1)(x\!+\!2)\cdots(x\!+\!n)}{(n+1)!}={x+n\choose n+1}) (coefficient binomial) pour tout
(coefficient binomial) pour tout  et tout
et tout  de
de 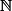 .
.
On considère la fonction
Puis, pour tout
Dans ce cas, on a
Modifié en dernier par Ben314 le 09 Fév 2016, 17:26, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
26 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

